Графический метод. Выбор оптимального варианта

С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линяя уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функции при графическом решении задач линейного программирования используют вектор  на плоскости , который обозначим . Этот вектор показывает направление наискорейшего изменения целевой функции, он равен

,

где  и  – единичные векторы по осям  и  соответственно.

Координаты вектора  являются коэффициенты целевой функции .

Алгоритм решения задач

1) Находим область допустимых решений системы ограничений задачи.

2) Строим вектор .

3) Проводим линию уровня , которая перпендикулярна .

4) Линию уровня перемещаем по направлению вектора  для задачи на максимум и в направлении, противоположном , для задачи на минимум.

Перемещение линий уровня производится до тех пор, пока у него не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи линейного программирования, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесчисленное множество решений. Говорят, что такая задача линейного программирования имеет альтернативный оптимум, и ее решение находится по формуле:

,

где ,

 и  – оптимальные решения в условиях ОДР.

Задача линейного программирования может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

5) Находим координаты точки экстремума и значение целевой функции в ней.

Пример 1. Для изготовления двух видов продукции  и  используют четыре вида ресурсов , . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице:

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы
		продукции	продукции
	18	1	3
	16	2	1
	5	-	1
	21	3	-

Прибыль, получаемая от единицы продукции  и , – соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение:

Составим экономико-математическую модель задачи. Обозначим  и – число единиц продукции соответственно  и , запланированных к производству. Связь между потреблением ресурсов и их запасами выразится системой неравенств

Суммарная прибыль  составляет  руб. от реализации продукции  и руб. – от реализации продукции , т.е. .

Итака, экономико-математическая модель задачи: при которой функция принимает максимальное значение.

Изобразим многогранник решений.

Построим вектор

Перемещая линию уровня в направлении вектора , найдем оптимальное решение в угловой точке 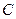, определяемое системой уравнений

откуда  т.е. .

Максимум линейной функции равен  т.е. максимальная прибыль в 24 руб. достигается при производстве 6 ед. продукции  и 4 ед. продукции .