Проекция вектора на ось

Пусть в пространстве задана ось l, т.е. направленная прямая.

 

Def.Проекцией точки М на ось l  называется основание М₁ перпендикуляра ММ₁, опущенного из точки на ось. Если точка М лежит на оси, то проекция точки на ось совпадает с М.

                                   М

 

                                    М₁                                 l

 

Пусть 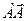 - произвольный ненулевой вектор.

 

Def.Проекцией вектора 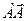 на ось l  называется скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительным направлением оси и вектора (или величина направленного отрезка A’B’ (где АA’^ l, BB’^ l).

Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол прямой. Таким образом, проекция вектора на ось – это число, равное длине отрезка А’В’, взятое со знаком «+», если направление A’B’ совпадает с направлением оси l, и со знаком «-», если эти направления противоположны.    

                                     В                                                                                                               

                                A 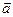                                   пр а_l = ‌ ç ç cos j

                           

                      A’       B’           

Проекции равных векторов равны между собой.

 

Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях единичные векторы (орты), обозначив их 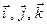 соответственно. Выберем произвольный вектор  пространства и совместим его начало с началом координат: .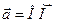

 

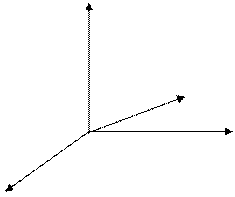Обозначим проекции вектора 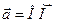 на оси координат Ox, Oy, Oz соответственно 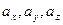, т.е. ,

                             ,

                             .

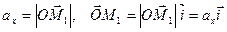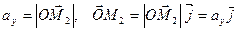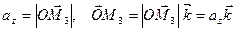Так как 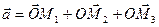, то

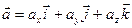        (4.1)

Формула (4.1) является основной в векторном исчислении и называется разложением вектора по ортам координатных осей.

Числа 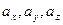 называются координатами вектора. Таким образом, координаты вектора есть его проекции на соответствующие координатные оси.

Равенство (4.1) можно записывать в виде: 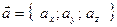         (4.2).

Def.Модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций на оси координат, т.е.

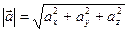(4.3)

 

Если a, b, g - соответственно углы, образованные вектором 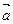 с координатными осями Ox, Oy, Oz прямоугольной системы координат, то по определению проекции вектора на ось имеем:

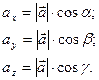  (4.4)

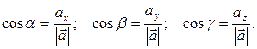Или                                   (4.5)

 

Def. Косинусы углов, образованных вектором с координатными осями, называются направляющими косинусами этого вектора.

 

Для них справедливо утверждение: сумма квадратов направляющих косинусов ненулевого вектора равна единице:

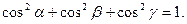          (4.6)