Смешанное произведение векторов

Def. Смешанным произведением трёх векторов 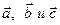 называется скалярное произведение вектора  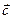на векторное произведение  и представляет собой скаляр вида

         (4.21),

где y - угол между векторами 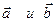; j - угол между векторами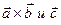  

Выражение смешанного произведения в координатной форме: если векторы заданы в координатной форме: 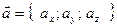, , 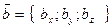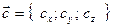то их смешанное произведение определяется формулой:

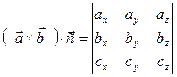         (4.22)

(т.е. смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов)

Свойства смешанного произведения:

1. При круговой перестановке сомножителей знак смешанного произведения не изменяется:

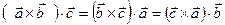
2. Смешанное произведение не изменяется при перемене местами знаков векторного и скалярного умножения, т.е.

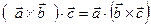
Некоторые приложения смешанного произведения:

1. Определение взаимной ориентации векторов в пространстве: если 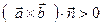, то векторы  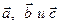образуют правую тройку векторов, а если , то левую тройку.

2. Условие компланарности векторов:

     векторы 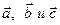компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е.

3. Объём параллелепипеда, построенного на векторах 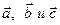, определяется по формуле:

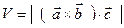(4.23)

4. Объём пирамиды, построенной на векторах , определяется по формуле:

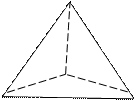
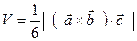(4.24)