2020-10-12
229
Def. Три некомпланарных вектора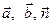 
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора 
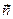кратчайший поворот от первого вектора 
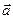ко второму вектору 
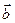виден совершающимся против часовой стрелки (и левую, если по часовой)
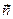
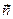
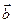
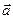
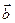
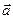
Def. Векторным произведением векторов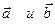 
называется вектор 
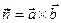, удовлетворяющий следующим условиям:
- его модуль вычисляется по формуле:
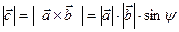, (4.17)
где y - угол между векторами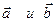 
;
- вектор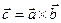 
перпендикулярен плоскости, определяемой перемножаемыми векторами (
);
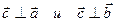- векторы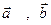 
и 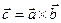образуют правую тройку векторов (направление вектора векторного произведения определяется по правилу «буравчика» (штопора): если вращать рукоятку буравчика в направлении от 
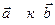, то буравчик будет двигаться в направлении вектора 
)
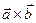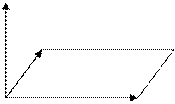
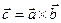
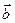
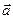
Выражение векторного произведения в координатной форме: если векторы заданы в координатной форме: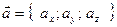 
, 
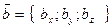, то координаты вектора их векторного произведения определяются из формулы:
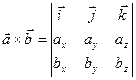(4.18)
Свойства векторного произведения:
1. При перестановке местами сомножителей векторное произведение меняет знак на противоположный (т.е. векторное произведение не обладает свойством переместительности):
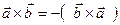
2. 
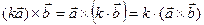- сочетательное свойство относительно скалярного множителя (постоянный множитель можно вынести за знак векторного произведения);
3. Распределительное свойство: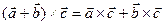 
;
Некоторые приложения векторного произведения:
1. Условие коллинеарности двух ненулевых векторов 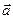и 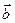имеет вид:
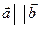Û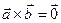 
(если векторы коллинеарны, то их векторное произведение равно нулевому вектору, и обратно, если векторное произведение ненулевых векторов равно нулевому вектору, то они коллинеарны).
2. Геометрические приложения векторного произведения:
а) площадь параллелограмма, построенного на векторах 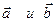как на сторонах, определяется как модуль их векторного произведения:
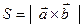(4.19)
б) площадь треугольника, построенного на векторах 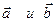как на сторонах, равен половине от модуля их векторного произведения:
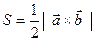(4.20)
