Определение деформации изгиба двухопорной балки.
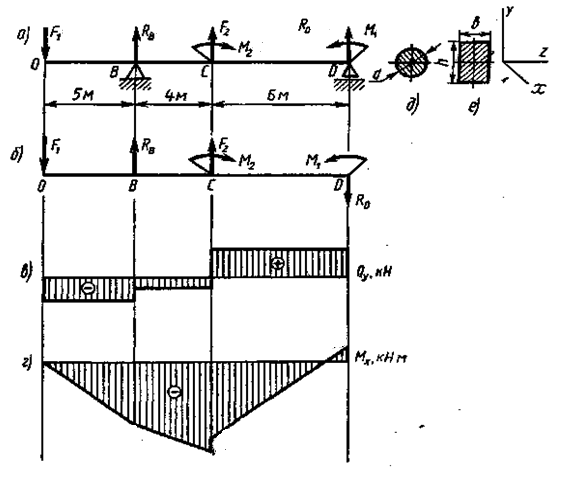
Для заданной двухопорной балки (рис. 18, а) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h, b, d) в форме прямоугольника, приняв для прямоугольника h/b = 1,5. Считать [ σ ] = 160 МПа.
Дано: F1 = кН; F2 = кН; М1 = кН м, М2= кНм,  = 10 кН,
= 10 кН, 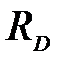 = 22 кН
= 22 кН
Найти: Qy; Mx; Wx подобрать сечение бруса
Решение.
1. Делим балку на участки по характерным сечениям О, В, С, D (рис. 18, б).
2. Определяем в характерных сечениях значения поперечной силы Qy
и строим эпюру слева направо (рис. 18, в):
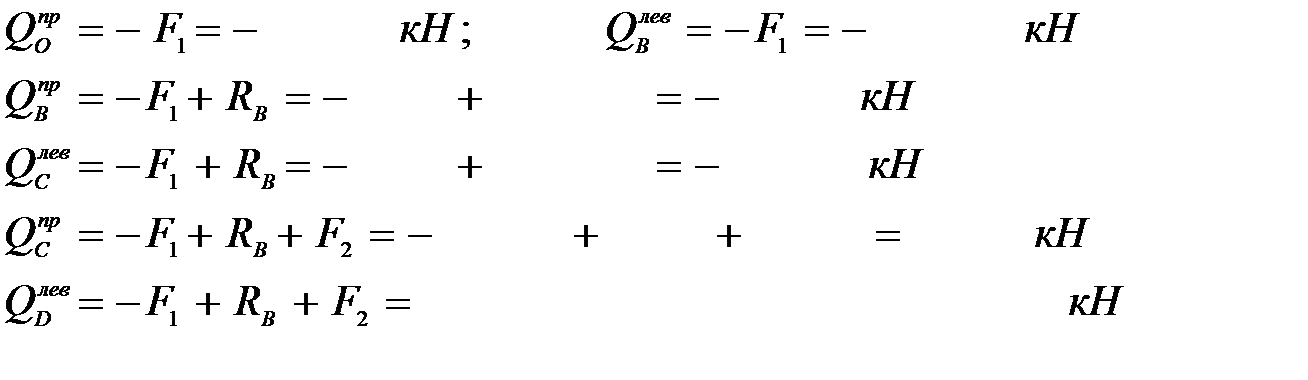
4. Вычисляем в характерных сечениях значения изгибающего момента Mx и строим эпюру (рис. 18, г):
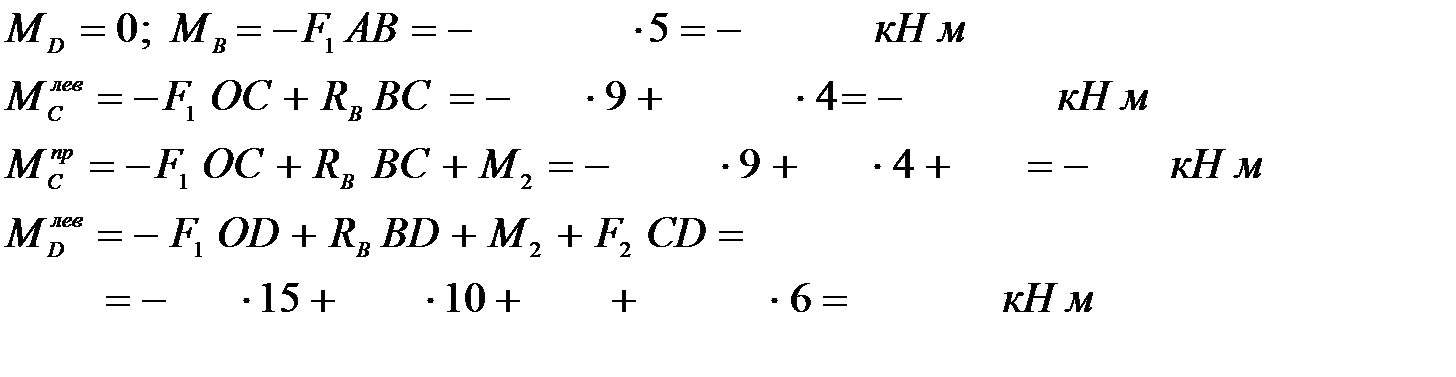
5. Вычисляем размеры сечения данной балки из условий прочности
на изгиб по двум вариантам: а) сечение - прямоугольник с заданным соотношением сторон (рис. 18, е) б) сечение - круг (рис. 18, д).
Вычисление размеров прямоугольного сечения:

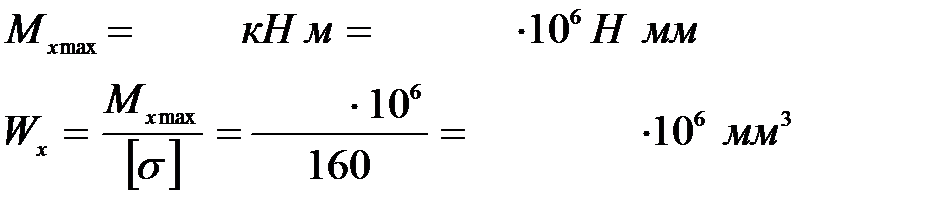
Используя формулу 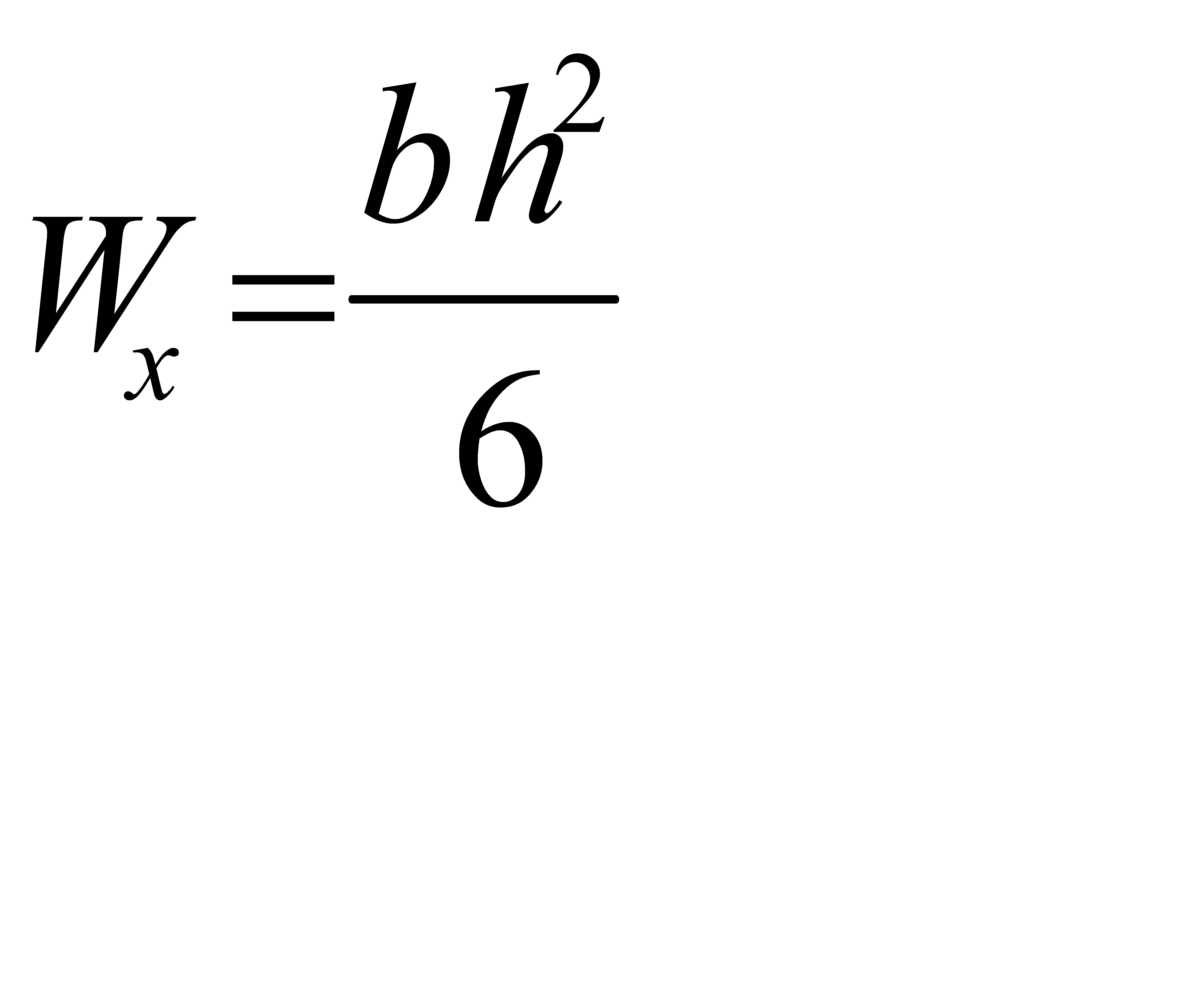 и учитывая, что h = 1,5b, находим
и учитывая, что h = 1,5b, находим
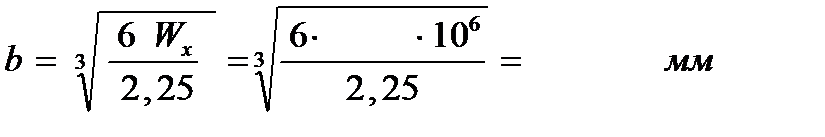
Варианты заданий
| № варианта | F1 кН | F2 кН | М1 кНм | М2 кНм | № варианта | F1 кН | F2 кН | М1 кНм | М2 кНм |
| 1 | 2 | 11 | 15 | 20 | 20 | 2 | 7 | 6 | 30 |
| 2 | 3 | 12 | 16 | 21 | 21 | 11 | 9 | 8 | 25 |
| 3 | 4 | 13 | 17 | 23 | 22 | 3 | 11 | 10 | 14 |
| 4 | 5 | 14 | 18 | 25 | 23 | 12 | 23 | 12 | 12 |
| 5 | 6 | 15 | 19 | 10 | 24 | 4 | 13 | 14 | 10 |
| 6 | 7 | 16 | 20 | 12 | 25 | 13 | 8 | 16 | 5 |
| 7 | 8 | 17 | 21 | 19 | 26 | 5 | 14 | 18 | 4 |
| 8 | 9 | 18 | 22 | 22 | 27 | 14 | 7 | 20 | 5 |
| 9 | 10 | 19 | 23 | 15 | 28 | 6 | 15 | 22 | 8 |
| 10 | 9 | 20 | 24 | 10 | 29 | 15 | 6 | 23 | 10 |
| 11 | 8 | 2 | 25 | 9 | 30 | 7 | 16 | 24 | 12 |
| 12 | 7 | 4 | 1 | 7 | 31 | 16 | 7 | 25 | 15 |
| 13 | 6 | 6 | 5 | 8 | 32 | 8 | 14 | 24 | 8 |
| 14 | 5 | 8 | 10 | 12 | 33 | 17 | 6 | 23 | 9 |
| 15 | 4 | 10 | 15 | 5 | 34 | 20 | 15 | 10 | 10 |
| 16 | 3 | 12 | 20 | 15 | 35 | 4 | 16 | 9 | 12 |
| 17 | 2 | 1 | 25 | 9 | 36 | 19 | 5 | 12 | 15 |
| 18 | 1 | 3 | 2 | 16 | 37 | 3 | 17 | 10 | 11 |
| 19 | 10 | 5 | 4 | 8 | 38 | 18 | 7 | 9 | 12 |
 2020-10-12
2020-10-12 627
627







