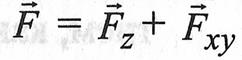 .
.
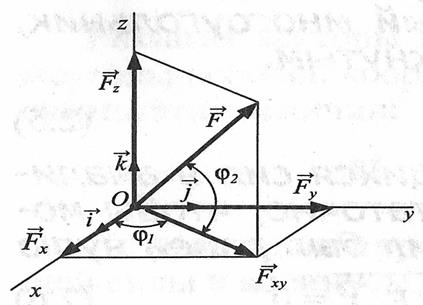
Проецируя векторы векторного равенства на координатные оси, имеем
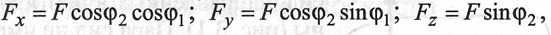
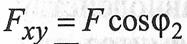 .
.

Рис. 2.3
При вычислении проекции силы на ось возможны следующие частные случаи:
1.Проекция положительна: 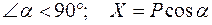 .
.
2. Проекция равна нулю: 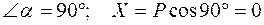 .
.
3. Проекция отрицательна: 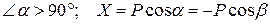 ,
,
где β - острый угол между линией действия силы и осью.
При решении задач рекомендуется вычислять абсолютное значение проекции силы как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции непосредственно по чертежу.
Условия и уравнения равновесия сходящейся системы сил
Сходящимися называются силы, линии действия которых пересекаются в одной точке.
Если к телу приложены две силы, линия действия которых пересекаются в одной точке, то их равнодействующая приложена в точке А пересечения линий действия сил; она изображается диагональю параллелограмма, построенного на этих силах (рис. 2.4). Построение параллелограмма сил можно заменить построением треугольника сил AВD (рис. 2.5).
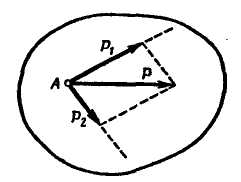
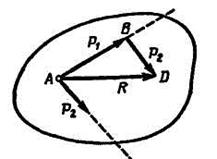
Рис. 2.4 Рис. 2.5
Направление равнодействующей силы 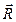 по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами.
по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами.
При помощи параллелограмма или треугольника сил можно решить и обратную задачу - разложить силу 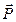 на две составляющие
на две составляющие 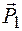 и
и 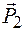 , приложенные в той же точке и направленные по заданным линиям действия KL и DE (рис. 2.6 и 2.7).
, приложенные в той же точке и направленные по заданным линиям действия KL и DE (рис. 2.6 и 2.7).
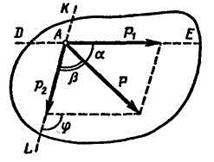
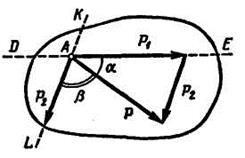
Рис. 2.6 Рис. 2.7
Используя известные формулы тригонометрии (теорему синусов), имеем:
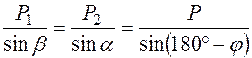 .
.
Так как 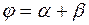 , то
, то
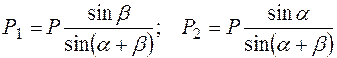 .
.
Векторная форма
Пусть к твердому телу в точках 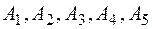 приложены сходящиеся силы
приложены сходящиеся силы 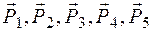 (рис. 2.8). Все эти силы можно перенести в точку О пересечения линий их действия и, строя треугольники сил, последовательно сложить. Тогда равнодействующая этих сил изобразится замыкающей стороной многоугольника сил.
(рис. 2.8). Все эти силы можно перенести в точку О пересечения линий их действия и, строя треугольники сил, последовательно сложить. Тогда равнодействующая этих сил изобразится замыкающей стороной многоугольника сил.
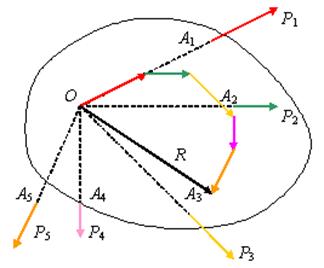
Рис. 2.8
Равнодействующая сходящихся сил приложена в точке О пересечения линий действия сил и равна их геометрической сумме:
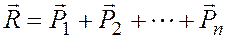 . (2.6)
. (2.6)
 2020-10-12
2020-10-12 582
582








