2020-10-12
252
ФЕРМА ТЕОРЕМА
Теорема Ферма - одна из первых теорем дифференциального исчисления, устанавливающая связь между поведением функции и значением ее производной. Пусть функция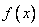 
определена на интервале 
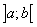и в некоторой точке 
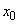этого интервала принимает наибольшее или наименьшее значение; если в этой точке существует производная 
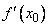, то она равна нулю: 
.
Геометрически это означает, что если в самой высокой или самой низкой точке графика функции, рассматриваемого на интервале 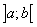, существует касательная, то эта касательная параллельна оси 
.
Теорема носит имя французского математика П. Ферма. Надо отметить, что сам Ферма не знал понятия производной, и теорема представляет уточнение его соображений и метода.
25. расчёт ферм способом сечения.
4.5.1. Способ замкнутого сечения
Пусть требуется определить усилия в стержнях фермы Шухова (рис.4.34,а). Применение способа вырезания узлов нецелесообразно, так как здесь нет узлов, в которых сходились бы только два стержня с неизвестными усилиями, и нельзя использовать способ проекций, так как невозможно провести сечение через три стержня.
а) 
б)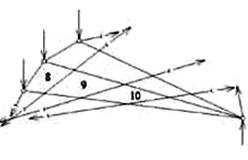 
Рис.4.34
Проведем замкнутое сечение так, чтобы три стержня (1, 4, 7) пересекались по одному разу, а стержни 8, 9, 10 – по два раза. Рассмотрим равновесие отсеченной части фермы внутри замкнутого контура (рис.4.34,б). Усилия в стержнях 8, 9, 10, перерезанных замкнутым сечением дважды, уравновешиваются. А усилия в стержнях 1, 4, 7 можно определить способом моментной точки, после чего легко определить усилия в остальных стержнях фермы.
