Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.
Условные выражения

характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.
Рассмотрим некоторые приемы раскрытия неопределенностей.
I. Неопределенность  .
.
1. 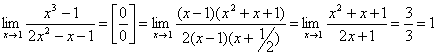 .
.
2. 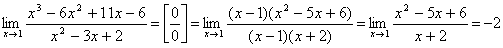 .
.
При разложении числителя на множители воспользовались правилом деления многочлена на многочлен «углом». Так как число x =1 является корнем многочлена x3 – 6 x2 + 11 x – 6, то при делении получим
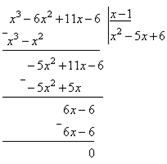
3. 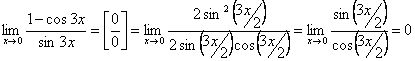
4. 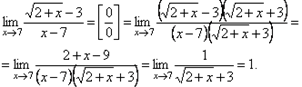 .
.
II. Неопределенность  .
.
1. 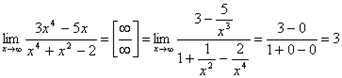 .
.
При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.
2. 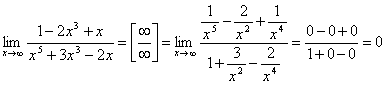 .
.
3. 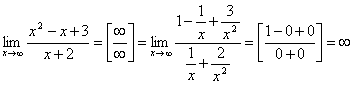 .
.
4.  .
.
При вычислении предела воспользовались равенством 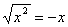 , если x< 0.
, если x< 0.
Следующие виды неопределенностей с помощью алгебраических преобразований функции, стоящей под знаком предела, сводят к одному из рассмотренных выше случаев  или
или  .
.
III. Неопределенность 0 ·∞.
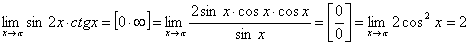 .
.
IV. Неопределенность ∞ –∞.
1. 
2. 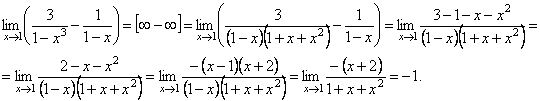
3. 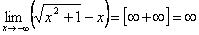 .
.
Замечательные пределы

Функция 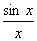 не определена при x =0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.
не определена при x =0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.
Однако, можно найти предел этой функции при х →0.
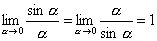
Выведенная формула и называется первым замечательным пределом.
Таким образом, первый замечательный предел служит для раскрытия неопределенности  . Заметим, что полученную формулу не следует путать с пределами
. Заметим, что полученную формулу не следует путать с пределами 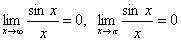 .
.
Примеры.
1.  .
.
2. 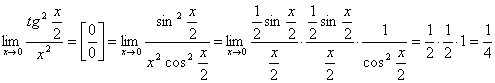 .
.
3.  .
.
4. 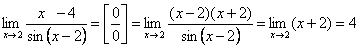 .
.
Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом

Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).
Примеры.
1. 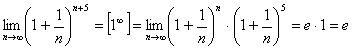 .
.
2.  .
.
3. 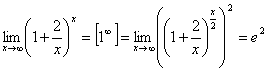 .
.
4. 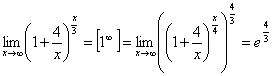 .
.
5. 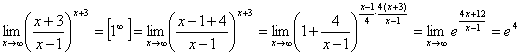 .
.
 2020-10-09
2020-10-09 876
876








