Скалярное произведение — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. 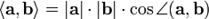 a*b={ax*bx + ay*by + az* bz}
a*b={ax*bx + ay*by + az* bz}
Если хотя бы один из векторов равен нулю, то скалярное произведение равно нулю.
Скалярное произведение в координатах
Если 
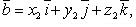 то
то 
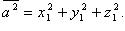
Ортогональность двух векторов
Для того, чтобы два вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю, то есть (х, у)=0.
(х, у)=0 – условие ортогональности двух векторов
Векторным произведением вектора
C = A x B
1) Вектор С действует вдоль прямой перпендикулярой A и B = > C перпендик. A и B
2) С по длине равен площади параллелограмма С = S = |A| * |B| sin α
3) A, B, C –правая тройка A x B = -B x A
Условие коллинеарности векторов
Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.
6. Смешанным произведением векторов 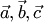 называется число
называется число 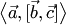 , равное скалярному произведению вектора
, равное скалярному произведению вектора  на векторное произведение векторов
на векторное произведение векторов  и
и 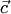 . Смешанное произведение обозначается
. Смешанное произведение обозначается 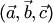 .
.
Условия компланарности
Три вектора  ,
, 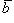 и
и 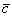 называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.
называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.
Линейная зависимость
Система векторов 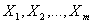 называется линейно зависимой, если найдутся числа
называется линейно зависимой, если найдутся числа 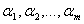 одновременно не равные нулю
одновременно не равные нулю  такие что
такие что 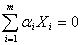 , где
, где  – это вектор с нулевыми координатами.
– это вектор с нулевыми координатами.
Сумму 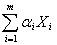 называем линейной комбинацией векторов
называем линейной комбинацией векторов 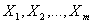 .
.
 2020-10-12
2020-10-12 156
156








