ЗАМЕЧАНИЕ Во всех задачах этого пункта будем считать, что дан ортонормированный базис
47. а (1,-1,3), в( 2,4,-5), с (1,-2,1). Найти: 1) а в, 2) | с |, 3) Соs 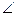 (в, с).
(в, с).
4) (а + в + 5 с) · ( 2 в -4 с), 5) (а – в) · (с – а).
48.В параллелограмме АВСД АВ (-8,0,6), ДА (-3,-4,0). Найти 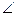 ВАД.
ВАД.
49. Найти косинусы углов, образованных вектором а (5, - 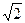 , 3)
, 3)
с базисными векторами i, j, k.
50. Дан тетраэдр АВСД. АВ (1,4,1), АС (2,-3,-2), АД (0,5,0). Найти Соs 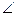 ВАМ, где М – середина СД.
ВАМ, где М – середина СД.
51. МАВСД – четырехугольная пирамида, основание которой – параллелограмм АВСД. К и Р – середины сторон АВ и ВС. ВА (6,0,-4), ВС (4,4,10), ВМ (1,-2,3). Найти 1) | АС |, 2) Соs 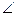 КМР.
КМР.
52. В пространственном четырехугольнике АВСД АВ (1,6,-2), ВС (5,3,-1), СД (1,-7,1). Доказать, что диагонали четырехугольника перпендикуляры.
53. Дан четырехугольник АВСД. АВ (6,0,-8), ВС (0,10,0), СД (-6,0,8). Доказать, что этот четырехугольник является квадратом.
54. Найти длину медианы АМ треугольника АВС и угол АМВ, если АВ (1,-1,2), АС (3,5,-4).
55. Объяснить, почему для любых векторов а, в, с не выполняется равенство (а в) с = а (в с)? Найти все векторы а, в, с д ля которых это равенство выполняется.
ЗАДАЧА № 11
АД – биссектриса треугольника АВС. Выразить вектор АД через векторы АВ и АС.
РЕШЕНИЕ.
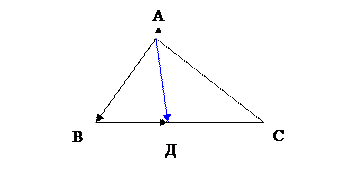
1) АД = АВ + ВД = АВ + х ВС = АВ + х (АС – АВ) или
АД = АВ + х (АС - АВ) (1)
2) Найдем коэффициент х, для которого ВД = х ВС. Так как векторы
ВД и ВС сонаправлены, то коэффициент х положителен. Из определения произведения вектора на число получим, что | ВД | =│х│ | ВС | = х | ВС |, а отсюда следует, что
х = 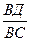 (2)
(2)
3) Так как АД – биссектриса треугольника АВС, то по свойству биссектрисы треугольника получаем, что
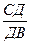 =
= 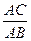 (3)
(3)
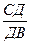 =
= 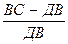 =
= 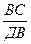 - 1 или
- 1 или
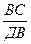 =
= 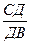 + 1 (4)
+ 1 (4)
Из (3) и (4) следует, что 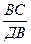 =
= 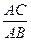 + 1 =
+ 1 = 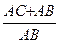 , отсюда и из (2) получаем, что х =
, отсюда и из (2) получаем, что х = 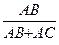 . Поставляем это значение х в (1) и получаем
. Поставляем это значение х в (1) и получаем
АД = АВ + 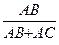 . (АС - АВ) = (1 -
. (АС - АВ) = (1 - 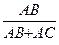 ) АВ +
) АВ + 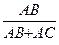 АС или
АС или
АД = 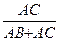 АВ +
АВ + 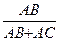 АС (5)
АС (5)
ОТВЕТ. Если АД - биссектриса треугольника АВС, то
АД = 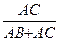 АВ +
АВ + 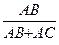 АС.
АС.
ЗАДАЧА № 12
АН – высота треугольника АВС. Выразить вектор АН через векторы АВ и АС.
РЕШЕНИЕ.
|

1) АН = АВ + ВН = АВ + х ВС = АВ + х (АС – АВ) или
АН = АВ + х (АС - АВ) (1)
2) Найдем коэффициент х, для которого ВН = х ВС.
Так какАН – высота треугольника АВС, то АН 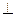 ВС, значит АН
ВС, значит АН 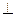 ВС, поэтому скалярное произведение АН ВС = 0. Подставим в это соотношение вместо АН его выражение из (1), получим
ВС, поэтому скалярное произведение АН ВС = 0. Подставим в это соотношение вместо АН его выражение из (1), получим
[ АВ + х (АС - АВ) ] ВС = 0, по свойству скалярного произведения можно раскрыть квадратные скобки АВ ВС + х (АС - АВ) ВС = 0, отсюда
АВ ВС АВ(АС-АВ)
х = ------------------- или х = - ----------------- (2)
(АС – АВ) ВС (АС _ АВ)2
Подставим это значение х в формулу (1), получим
АВ(АС-АВ)
АН = АВ - ---------------- (АС – АВ) (3)
(АС – АВ)2
ОТВЕТ. Если АН –высота треугольника АВС, ТО
АВ(АС –АВ)
АН = АВ - ----------------- (АС – АВ)
(АС – АВ)2
ЗАМЕЧАНИЕ.
1) Если вам хочется упростить формулу (2), то этого делать нельзя, т.к если числитель и знаменатель дроби есть скалярные произведения а в и в в, то это числа, равные произведению длин векторов на косинус угла между ними, кроме того в векторной алгебре нет действия деления вектор на вектор. 
2) Если вам хочется упростить формулу (3), то этого делать нельзя, т.к
второе слагаемое можно переписать так:
[ АВ(АС –АВ) ](АС - АВ)
------------------------------------- ,
(АС –АВ) 2
но для скалярного произведения [ а в ] с 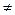 а [ в с ]., поэтому квадратные скобки во втором слагаемом формулы (3) переставить нельзя.
а [ в с ]., поэтому квадратные скобки во втором слагаемом формулы (3) переставить нельзя.
ЗАДАЧА № 13
Дан ортонормированный базис. В треугольнике АВС АВ (3,0,4), АС (8,0,-6) Найти а) длину высоты АН, б) угол между медианой АМ и биссектрисой АД.
РЕШЕНИЕ
1) Найдем координаты вектора АН и его длину. По задаче № 10
АВ(АС-АВ)
АН = АВ - ------------------ (АС – АВ). Сначала найдем, чему равно число х=
(АС – АВ)2
АВ(АС-АВ)
(АС – АВ)2. Так как АВ (3,0, 4) АС (8, 0,-6), то (АС – АВ)(5,0,-10), то
х = 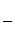
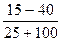 =
= 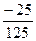 =
= 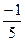 .
.
Тогда АН = АВ + 1/5 (АС – АВ), отсюда найдем координаты вектора АН.
АН( 4, 0, 2), тогда │ АН │= 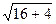 = 2
= 2 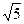

АМ АД
2) Воспользуемся формулой Соs 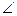 МАД = | АМ | | АД |
МАД = | АМ | | АД |
3) Найдем координаты вектора АМ и его длину . Так как АМ = ½ (АВ + АВ), то АМ (5/2, 3, 2) и | АМ | = 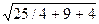 =
= 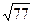 /2.
/2.
4)Найдем координаты вектора АД и его длину.
По задаче № 9 АД = 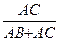 АВ +
АВ + 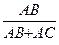 АС.
АС.
Так как АВ (3,0,4) АС (8, 0,-6), поэтому АВ =│АВ│= 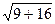 = 5, АС=│АС│=
= 5, АС=│АС│= 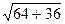 =10, тогда АД = 2/3 АВ + 1/3 АС, поэтому
=10, тогда АД = 2/3 АВ + 1/3 АС, поэтому
АД (14 / 3, 0, 2 / 3)
и │ АД │= 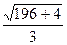 =
= 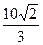
АМ АД 70/6 + 0 + 4/3 39 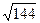
5) Соs 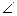 МАД = | АМ | | АД | = 10
МАД = | АМ | | АД | = 10 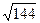 /6 = 720
/6 = 720
ОТВЕТ. |АМ| = 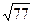 / 2, Соs
/ 2, Соs 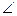 МАД = 39
МАД = 39 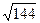
720
56. Найти длины медианы АД и высоты АН треугольника АВС, если АВ (0,4,0), АС (-3, 0,0).
57. В треугольнике АВС АВ (2,1,3), АС (0,1,1) Найти косинус угла между медианой АМ и высотой АН.
58. АМ и АД медиана и биссектриса треугольника АВС. Найти косинус угла МАД, если АВ (0,4,0), АС (-3, 0,0).
59. В треугольнике АВС АМ - медиана, АД –биссектриса, АН – высота. Найти длину АМ и косинус угла НАД, если АВ (2,0,0), АС (0,0,4).
 2020-10-12
2020-10-12 195
195








