Пусть 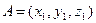 и
и 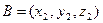 . Имеем
. Имеем 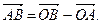
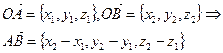 (3.1).
(3.1).
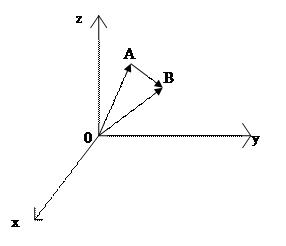 Таким образом, координаты вектора можно найти, вычитая из координат конечной точки соответствующие координаты начальной точки вектора.
Таким образом, координаты вектора можно найти, вычитая из координат конечной точки соответствующие координаты начальной точки вектора.
Пример 3.1. Пусть даны координаты точек 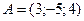 и
и  . Найдем координаты вектора
. Найдем координаты вектора 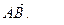
Решение. Используем формулу (3.1): 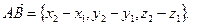
Тогда 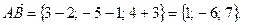
Линейные операции над векторами в координатной форме
Пусть 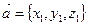 и
и 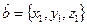
Тогда
1)  ;
;
2)  ;
;
3)  т.е.
т.е. 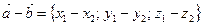 .
.
Пример. 3.2. Найти координаты вектора 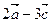 , если
, если 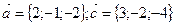 .
.
Решение. 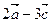
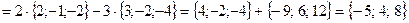 .
.
Условие коллинеарности ( параллельности) векторов
Для параллельности двух векторов необходимо и достаточно, чтобы координаты одного вектора были пропорциональны координатам другого
Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.
Формулы (1) и (2) кратко записывают в виде следующих пропорций:
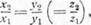 соответственно
соответственно 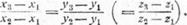
Здесь один из знаменателей может оказаться равным нулю. Чтобы обойти эту трудность, договоримся всякую пропорцию понимать в смысле равенства ad = bс. Тогда обращение в нуль одного из знаменателей означает обращение в нуль и соответствующего числителя.
При этом обращение какого-нибудь из знаменателей в нуль означает, в соответствии с равенствами (1) или (2), что и числитель этой дроби равен нулю.
Понимать эти равенства надо с таким условием: если какой-то знаменатель равен нулю, то равен нулю и соответствующий числитель (про пропорциональность).
Из формулы вычеркиваются те из отношений, знаменатели которых равны нулю, а числители вычеркнутых отношений приравниваются нулю.
Длина (модуль) вектора заданного координатами
Если 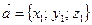 , то длина (модуль) вектора:
, то длина (модуль) вектора:
 (3.2).
(3.2).
Расстояние между двумя точками 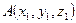 и
и 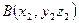
АВ = 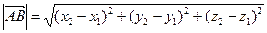 (3.3).
(3.3).
Пример 3.3. Даны координаты точек 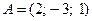 и
и 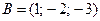 . Найти расстояние между ними.
. Найти расстояние между ними.
Направляющие косинусы вектора
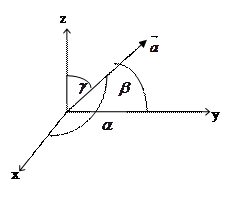 Пусть
Пусть 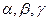 – углы, которые образует вектор
– углы, которые образует вектор 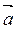 с осями координат Ox, Oy, Oz соответственно.
с осями координат Ox, Oy, Oz соответственно.
Тогда 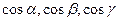 называются направляющимися косинусами вектора
называются направляющимися косинусами вектора 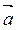 :
:
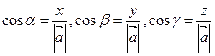 (3.4).
(3.4).
Следствия:
1) 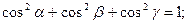
2) 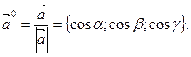
 2020-10-12
2020-10-12 173
173








