1. Найти все значения m, при которых длина вектора  = (m
= (m 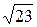 , 5, 4) больше 8.
, 5, 4) больше 8.
2. Найти длину вектора  по заданным координатам его концов
по заданным координатам его концов
А (2; 3; 1) и В (1; 1; 3).
3. В равнобедренном треугольнике с вершинами в точках А (4; 2; 1),
В (6; 3; 2), С (3; 4; 0) найти длину боковой стороны.
4. При каких значениях k, m векторы 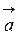 = (1, m, 2) и
= (1, m, 2) и  = (4, 1, k) коллинеарны?
= (4, 1, k) коллинеарны?
5. Даны векторы  = (2; -4; 6) и
= (2; -4; 6) и  = (m; 2; n). Найти сумму m + n, если точки А, В и С лежат на одной прямой.
= (m; 2; n). Найти сумму m + n, если точки А, В и С лежат на одной прямой.
6. Известно, что вектор  направлен противоположно вектору
направлен противоположно вектору  = (-18; 9; - 6) и |
= (-18; 9; - 6) и | 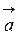 | = 7. Найти сумму координат вектора
| = 7. Найти сумму координат вектора 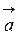 .
.
7. При каких значениях m векторы 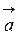 = (m
= (m  , - 5, 1) и
, - 5, 1) и  = (1, 1, - 4) перпендикулярны?
= (1, 1, - 4) перпендикулярны?
8. Найти косинус угла между векторами 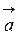 = (3, 2, 1) и
= (3, 2, 1) и  = (1, 1, 2).
= (1, 1, 2).
9. Точки А (2; 3; -5), С (3; 6; 8) и D (5; 4; -1) являются вершинами параллелограмма ABCD. Найти длину диагонали BD.
10. Точки А (1; 3; -1), В (2; 4; 5) и С (8; 5; 6) являются вершинами ромба ABCD. Найти длину диагонали BD.
11. Найти градусную меру угла между вектором  = (-
= (-  ; -
; -  ;
;  ) и осью абсцисс.
) и осью абсцисс.
12. Найти градусную меру угла между вектором  = (-1;
= (-1; 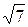 ; -2
; -2 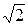 ) и осью Oz.
) и осью Oz.
13. Найти |  |, если |
|, если | 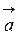 | =
| = 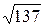 ,
,  = 20 и
= 20 и  = 18.
= 18.
14. Найти 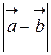 , если |
, если | 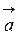 | = 17,
| = 17, 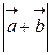 = 28 и |
= 28 и |  |= 21.
|= 21.
15. Найти градусную меру угла между векторами  и
и  , если
, если 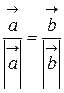
16. Найти | 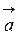 |• |
|• |  |, если вектор
|, если вектор 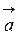 +
+  делит угол между векторами
делит угол между векторами
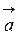 = (3; 5; - 7) и
= (3; 5; - 7) и  пополам.
пополам.
17. Найти градусную меру угла между векторами  ,
,  , если
, если
 = |
= | 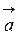 | + |
| + |  |.
|.
18. Даны векторы 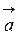 = (5; -2; 3),
= (5; -2; 3),  = (2; -3; 1) и
= (2; -3; 1) и  =
=  - 2
- 2  . Найти угол между векторами
. Найти угол между векторами 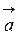 и
и  .
.
19. Даны векторы 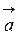 (3; 2; - 1) и
(3; 2; - 1) и  (2; 4; 1). Найти угол между векторами
(2; 4; 1). Найти угол между векторами 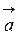 +
+  и
и 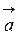 -
-  .
.
20. В параллелограмме ABCD известны векторы  = (-4;-4;3),
= (-4;-4;3),
 = (-2;-6;1) и вершина А (3; 7; -5). Найти сумму координат точки пересечения диагоналей параллелограмма.
= (-2;-6;1) и вершина А (3; 7; -5). Найти сумму координат точки пересечения диагоналей параллелограмма.
Ответы:
1. (-  ; -1)U(1; + ; -1)U(1; +  ); );
| 2. 3; | 3.  ; ;
|
| 4. k = 8, m = 1/4 | 5. -4; | 6. 5; |
7.±3; 8.  /6;
11. 120°; 12. 135°;
15. 0°; 16. 83; /6;
11. 120°; 12. 135°;
15. 0°; 16. 83;
| 9.  ;
13. 15;
17. 0°; ;
13. 15;
17. 0°;
| 10. 5 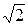 ;
14. 26;
18. 90°; ;
14. 26;
18. 90°;
|
19. 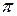 - arccos7/3 - arccos7/3  ; ;
| 20. 6. | - |
(Соболь Б.)Примеры 1-20
Пример 1. Найти все значения m, при которых длина вектора
 = (
= ( , -m, 2) равна 10.
, -m, 2) равна 10.
Ответ: т = ±9.
Пример 2. Найти все значения 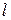 , при которых длина вектора
, при которых длина вектора
 = (
= (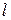 , 75, 4) больше 5.
, 75, 4) больше 5.
Ответ: (-  ; -2) и (2; +
; -2) и (2; +  ).
).
Пример 3. Найти длину вектора  по заданным координатам его концов А (4, 3, -1); В (1-, 6, 2).
по заданным координатам его концов А (4, 3, -1); В (1-, 6, 2).
Пример 4. Найти длину основания равнобедренного треугольника с вершинами в точках А (2; 3; 1), В(1; 3; 3) и С(2; 4; 3).
Ответ: 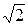 .
.
Пример 5. Даны векторы  = (3; 5; 1),
= (3; 5; 1),  = (1; 4; 2) и
= (1; 4; 2) и 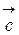 =
= 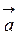 – 3
– 3 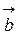 . Определить длину вектора с.
. Определить длину вектора с.
Ответ:  .
.
Пример 6. При каких значениях k, m векторы  = (-1, - 1, т) и
= (-1, - 1, т) и 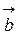 = (к, 4, 5) коллинеарны?
= (к, 4, 5) коллинеарны?
Ответ: k = 4, m = - 5/4
Пример 7. Даны векторы  = (-3; 5; 11) и
= (-3; 5; 11) и  = (6; m; n). Найти разность m - n, если точки A, B, C лежат на одной прямой.
= (6; m; n). Найти разность m - n, если точки A, B, C лежат на одной прямой.
Ответ: 12.
Пример 8. Даны векторы  = (2; 4; -1),
= (2; 4; -1),  = (3; 5; -3) и
= (3; 5; -3) и 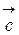 = 2
= 2 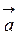 -
- 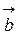 . Найти скалярное произведение векторов
. Найти скалярное произведение векторов  и
и  .
.
Ответ: 13.
Пример 9. При каких значениях 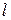 векторы
векторы  = (5,
= (5, 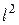 , 14)
, 14)
и  = (2, 1, -1) перпендикулярны?
= (2, 1, -1) перпендикулярны?
Ответ: ±2.
Пример 10. Найти косинус угла между векторами 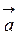 = (-1, 1, 1) и
= (-1, 1, 1) и
 = (-1, 5, 3).
= (-1, 5, 3).
Ответ:  .
.
Пример 11. Найти все значения m, при которых угол между векторами 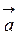 = (7; -1; 2т) и
= (7; -1; 2т) и  = (-2; 4m; 1) острый.
= (-2; 4m; 1) острый.
Ответ: m < -7.
Пример 12. В параллелограмме ABCD заданы вершина С(6; -8, 5) и векторы 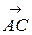 (-3; 1; 4) и
(-3; 1; 4) и  (2; - 3; 5) его диагонали. Найти сумму координат точки B.
(2; - 3; 5) его диагонали. Найти сумму координат точки B.
Ответ: 0.
Пример 13. Векторы  = (5; 2; -1) и
= (5; 2; -1) и  = (1; -5; -2), проведенные из точки С (5; 4; -3), являются боковыми сторонами равнобедренного треугольника. Найти сумму координат основания высоты треугольника, проведенной из вершины С.
= (1; -5; -2), проведенные из точки С (5; 4; -3), являются боковыми сторонами равнобедренного треугольника. Найти сумму координат основания высоты треугольника, проведенной из вершины С.
Ответ: 6.
 Пример 14. В треугольнике ABC заданы
Пример 14. В треугольнике ABC заданы  = (3; - 5; 2), точки М, N - середины сторон АВ и ВС соответственно, a
= (3; - 5; 2), точки М, N - середины сторон АВ и ВС соответственно, a  = (-4; 1; 7). Найти сумму координат вектора ВС.
= (-4; 1; 7). Найти сумму координат вектора ВС.
Ответ: 8
Пример 15. Вектор  направлен одинаково с вектором
направлен одинаково с вектором 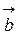 = (-8; 16; 4) и
= (-8; 16; 4) и
|  | =
| =  . Найти произведение координат вектора
. Найти произведение координат вектора 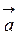 .
.
Ответ: -8.
Пример 16. Вектор  направлен противоположно вектору
направлен противоположно вектору  (3; - 4; -1) и |
(3; - 4; -1) и |  | = 3
| = 3 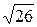 . Найти сумму координат вектора
. Найти сумму координат вектора  .
.
Ответ: 6
Пример 17. Точки А(4; -3; 7), В(5; 3; 8) и D(10; -4; 6) являются вершинами ромба ABCD. Найти длину диагонали АС.
Ответ:  .
.
Пример 18. Найти |  | + |
| + |  |, если |
|, если |  +
+  | = 19, |
| = 19, | 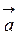 -
- 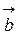 | = 17 и |
| = 17 и | 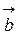 | = 10.
| = 10.
Ответ: 25.
Пример 19. Укажите градусную меру угла между вектором
 = (-
= (-  ; - 3
; - 3 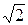 ; - 2
; - 2  ) и осью ординат.
) и осью ординат.
Ответ: 135°.
Пример 20. Найти |  | - |
| - |  |, если вектор
|, если вектор  +
+  делит угол между векторами
делит угол между векторами  = (23; -17; 88) и
= (23; -17; 88) и  пополам.
пополам.
Ответ: 0.
Тема. «Элементы векторной алгебры»
1. Что такое скалярные и векторные величины, привести их примеры и дать определение вектора.
2. Дать определения коллинеарных, компланарных векторов.
3. Дать определения равных, противоположных векторов.
4. Что относится к линейным операциям над векторами? Рассмотреть сложение векторов геометрическими методами с показом на примерах.
5. Дать определение разности двух векторов и привести геометрические методы вычитания векторов.
6. Дать определение произведения вектора на скаляр (число) и как выполняется эта операция геометрическим построением, привести пример.
7. Дать определение компоненты и проекции (координаты) вектора 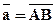 на координатную ось Ох. Привести формулы определения проекции вектора и её связи с компонентой.
на координатную ось Ох. Привести формулы определения проекции вектора и её связи с компонентой.
8. Дать линейные операции над векторами (сложение, вычитание и умножение вектора на скаляр) в координатной форме.
9. Дать определение коллинеарности векторов и привести условие коллинеарности в координатной форме.
10. Дать определение модуля и привести формулы вычисления модуля и направляющих косинусов вектора в пространстве.
11. Дать определение скалярного произведения векторов и привести его выражение через проекции вектора.
12. Привести скалярное произведение векторов в координатной форме и дать условие ортогональности векторов.
13. Дать определение векторного произведения, привести свойства его, привести его координатную форму и геометрический смысл.
14. Дать определение смешанного (векторно-скалярного) произведения трех векторов, привести его координатную форму и геометрический смысл.
 2020-10-12
2020-10-12 216
216








