2020-10-12
189
Скалярным произведением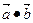 
двух векторов 
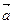и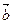 
называется число, равное произведению длин этих векторов на косинус угла между ними:
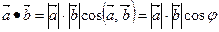(3.5).
Свойства скалярного произведения векторов:
1. 
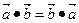
| 4.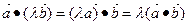 
|
2. 
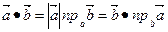
| 5. 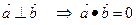 Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
|
3. 
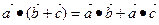
| 6.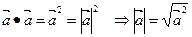 
|
Проекцией вектора 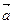на вектор 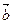называется число, равное
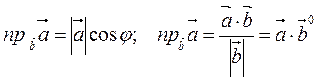(3.6).
Нахождение скалярного произведения через координаты векторов
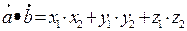(3.7).
Пример 3.4. Даны координаты векторов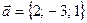 
и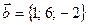 
. Найти их скалярное произведение.
Решение. По формуле (3.7) получим: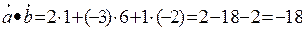 
.
Приложения скалярного произведения векторов
1) Если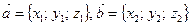 
, то угол между ними:
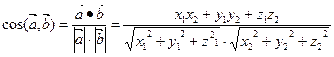(3.8).
2) 
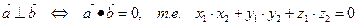(3.9).
Пример 3.5. Даны координаты векторов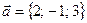 
и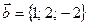 
. Найти косинус угла между ними.
Векторное произведение векторов
Векторным произведением двух векторов 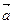и 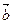называется третий вектор 
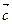, удовлетворяющий следующим трем условиям:
|
|
|
1) 
;
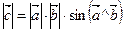2) 
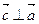и 
;
3) вектора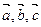 
образуют правую тройку (т.е. если смотреть с конца вектора 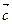, то кротчайший поворот от вектора 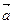к вектору 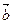совершается против часовой стрелки).
Векторное произведение обозначается: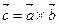 
.
Свойства векторного произведениявекторов:
1. 
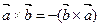
| 4.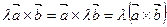 
|
2. 
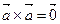
| 5. 
|
3. 
|
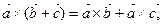
Нахождение векторного произведения через координаты векторов
Если 
и 
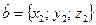, то
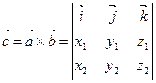(3.10).
или 
= 
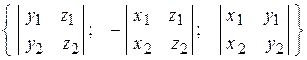(3.11).
Приложения векторного произведения векторов
1) Площадь параллелограмма построенного на векторах 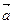и :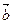
Sпарал.=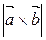 
(3.12).
2) Площадь треугольника построенного на векторах 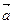и :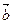
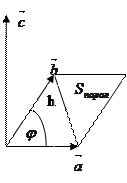
Sтреуг.=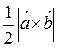 
(3.13).
Пример 3.6. Найти площадь параллелограмма построенного на векторах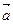 
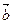и , где 
, 
.
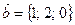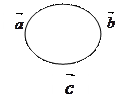
Смешанное произведение векторов
Смешанным произведением трёх векторов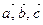 
называется число равное скалярному произведению вектора 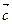на векторное произведение векторов 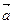и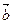
Смешанное произведение обозначается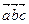 
и по определению равно:
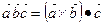(3.14).
Свойства смешанного произведения векторов:
1. 
;
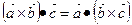2. 
;
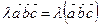3. 
;
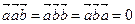4. 
;
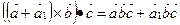5. 
(не нарушается круговой порядок);
6. 
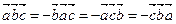(нарушается круговой порядок).
Нахождение смешанного произведения через координаты векторов
Если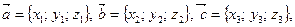 
то
(3.15).
