Свободные, скользящие и фиксированные векторы

Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).

Вместо определения 2 можно ввести другое определение ра­венства векторов, согласно которому векторы равны, если они равны по длине, лежат на одной прямой и направлены в одну сторону. В этом случае вектор может быть перенесен не в любую точку пространст­ва, а только вдоль прямой, на которой он лежит. При таком понимании равенства векторы называются скользящими векторами. В механике сила, действующая на абсолютно твердое тело, изображается сколь­зящим вектором, при этом известно, что две силы, равные и расположенные на одной прямой, оказывают на твёрдое тело одинаковое механическое действие.

Можно для векторов не вводить никакого особого понятия ра­венства, т. е. считать, что каждый вектор равен только самому себе и характеризуется, помимо длины и направления в пространстве, еще и точкой приложения. В этом случае векторы называются приложенными (связанными, «фиксированными» ) векторами. Как уже упоминалось, сила, действующая на нетвердое (например, упругое) тело, изображается приложенным вектором.

Если нужно подчеркнуть, что равенство понимается в смысле определения 2, то вектор называется свободным. Свободным вектором изображается, например, угловая скорость тела. Определение 3 определяет свободный вектор. Равные векторы отличаются друг от друга только положением начала. Однако во многих вопросах положение начала вектора не играет роли, существенны лишь длина и напра­вление вектора. Отвлекаясь в определении вектора от положения его начала, мы приходим к понятию свободного вектора. Таким образом, свободный вектор (в пространстве, на плоскости, на прямой) вполне определяется заданием его длины и (если он ненулевой) направления. Равные векторы, не совпадающие по положению, рассматриваются как разные конкретные изображения одного и того же свободного вектора.

Так в арифметике все равные между собой дроби рассматривают как разные изображения одного и того же рационального числа. При этом в арифметике настолько привыкли отождествлять дробь с изображаемым ею числом, что самые рациональные числа называют дробями. Подобно этому в векторном исчислении свободный вектор называют просто вектором. Мы также в дальнейшем почти всегда, будем пользоваться лишь термином вектор; при этом надо иметь в виду, что всюду, где специально не указано положение начала, речь идет о свободном векторе. Указывая начало, т. е. выбирая некоторое определенное изображение данного (свободного) вектора, мы будем говорить, что откладываем этот вектор от данной точки или совмещаем его начало с этой точкой и т. п.

Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными.

Вектор, противоположный вектору 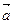, обозначается – 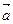. Для вектора  противоположным будет вектор . Вектор  называют противоположным вектору .

Определение. Говорят, что свободные векторы  и 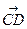  равны, если найдутся точки Е и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.

• Замечание. «Ухищрение» в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:

Определение. Говорят, что свободные векторы 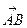 и , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.

Определение. Говорят, что скользящие векторы 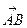 и 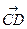равны, если

• точки A, B, C, D располагаются на одной прямой,

• векторы 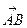 и 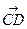 равны между собой как свободные векторы.

Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.

•     Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на которой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.

Иными словами, мы будем считать вполне тождественными (или эквивалентными) векторы, равные между собою.

Надо, однако, заметить, что в очень многих вопросах чистой и прикладной математики приходится рассматривать векторы, положение начала которых играет существенную роль. В отличие от последних векторы, только что охарактеризованные нами (т. е. такие, положение начала которых не играет никакой роли), назы­ваются свободными.

Из несвободных векторов в математике, механике и физике рассматриваются векторы скользящие и связанные.

Скользящие — это такие векторы, которые считаются тождествен­ными (эквивалентными), если они не только равны, но и распо­ложены на одной и той же прямой. Примером скользящего вектора может служить сила, приложенная к абсолютно твердому телу. Действительно, из механики известно, что две силы, равные и рас­положенные на одной прямой, эквивалентны в том смысле, что оказывают на твердое тело одинаковое механическое действие.

Связанные — это такие векторы, которые считаются тождест­венными, если они не только равны, но и имеют одинаковые начала. Примером связанного вектора может служить сила, приложенная к некоторой точке нетвердого (например, упругого) тела.

Определение. Говорят, что фиксированные векторы 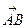 и 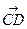 равны, если попарно совпадают точки А и С, В и D.

 

Метод координат

В элементарной (школьной) геометрии изучаются свойства прямолинейных фи­гур и окружности (в разделе планиметрия), а также прямые и плоскости в про­странстве, многогранники и круглые тела — цилиндр, конус, шар (в разделе сте­реометрия). Основную роль при этом играют построения, а вычислениям отводится роль вспомогательная. Выбор того или иного построения для каждого конкрет­ного случая требует обычно индивидуального подхода и соответствующей изобре­тательности, что и составляет основную трудность при решении задач методами элементарной геометрии.

Аналитическая геометрия и была призвана устранить эти трудности и создать единый метод решения различных геометрических задач. Поставленная цель была достигнута разработкой координатного метода, в котором основную роль играют вычисления, выполняемые по заданным формулам, а построения имеют вспомога­тельное значение.

Необходимые предпосылки для создания метода координат были подготовлены еще трудами древнегреческих математиков, в особенности Аполлония Пергского (ок. 260—170 до н. э.). Однако систематическое развитие этот метод получил в первой половине XVII века в работах Рене Декарта и Пье­ра Ферма.

Рене Декарт (Rene Descartes, 1596—1650) — знаменитый французский фи­лософ, математик, физик и физиолог. Родился в г. Лаэ (департамент Турень) в дворянской семье. В 1629 г. поселился в Голландии, где написал большую часть своих работ. Умер в Стокгольме, куда переехал в 1649 г.

В физике Декарт установил закон преломления света на границе двух сред (который несколько раньше и независимо от него был сформулирован В. Снеллиусом), пояснил образование радуги. Ему же принадлежит формулировка закона сохра­нения количества движения (в скалярной форме) и разработка механистической гипо­тезы образования тел Солнечной системы. В области физиологии Декарту принадле­жит большое число экспериментов и ряд плодотворных научных идей, в частности, он первым ввел понятие о рефлексе.

В 1637 г. Декарт издал большой философский трактат «Рассуждение о мето­де. С приложениями: Диоптрика, Метеоры, Геометрия» (русский перевод, Гостехиздат, М., 1953), в котором, в частности, систематически изложен метод прямоли­нейных координат, введена удобная алгебраическая символика, сохранившаяся до наших дней, выполнена классификация кривых на алгебраические и трансцен­дентные, а также даны способы построения касательных и нормалей к плоским алгебраическим кривым. Благодаря этой работе, которая оказала большое влияние на дальнейшее развитие математики, Декарта, наряду с его не менее знаменитым соотечественником Ферма (который раньше и более последовательно, чем Декарт, разработал метод координат, но работы Ферма, в том числе и по аналитической геометрии, были опубликованы только в 1679 г. после его смерти), и считают основоположником аналитической геометрии, а 1637 год — годом ее зарождения.

Перейдём к изложению метода координат.