Электростатика
Задача 1. Определить ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон ( кг,
кг,  Кл), чтобы его скорость возросла от
Кл), чтобы его скорость возросла от  до
до  . Значения
. Значения  и
и  приведены в таблице.
приведены в таблице.
| Заданные величины | номер варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| n1, м/с | 1,0.106 | 0,5.106 | 1,2.106 | 0,1.106 | 0,7.106 | 2,2.106 | 3,0.106 | 1,6.106 | 1,9.106 | 2,2.106 |
| n2, м/с | 2,3.106 | 0,9.106 | 1,9.106 | 0,5.106 | 2,3.106 | 4,5.106 | 5,1.106 | 3,0.106 | 3,3.106 | 4,4.106 |
Решение. Работа, совершаемая силами электростатического поля при перемещении электрона из точки 1 в точку 2, определяется формулой:
 . (1)
. (1)
С другой стороны, эта работа равна изменению кинетической энергии электрона:
 . (2)
. (2)
Приравняв выражения (1) и (2), найдем искомую ускоряющую разность потенциалов:
 .
.
Задача 2. Найти объемную плотность энергии  электрического поля вблизи точки, находящейся на расстоянии
электрического поля вблизи точки, находящейся на расстоянии  от поверхности заряженного шара радиусом
от поверхности заряженного шара радиусом  . Поверхностная плотность заряда на шаре
. Поверхностная плотность заряда на шаре  , диэлектрическая проницаемость среды
, диэлектрическая проницаемость среды  , значения параметров
, значения параметров  ,
,  ,
,  и
и  приведены в таблице.
приведены в таблице.
| Заданные величины | номер варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x, см | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |

| 2,0 | 3,5 | 2,5 | 1,7 | 1,9 | 0,9 | 6,3 | 3,4 | 7,0 | 2,0 |
| R, см | 1,8 | 1,0 | 1,2 | 2,4 | 1,6 | 2,5 | 3,3 | 1,1 | 0,9 | 2,7 |
| s, мкКл/м2 | 12,5 | 15,0 | 17,5 | 20,0 | 22,0 | 25,0 | 27,0 | 33,0 | 30,5 | 10,0 |
Решение. Объемная плотность энергии определяется выражением:  .
.
Напряженность поля на расстоянии  от поверхности заряженного шара
от поверхности заряженного шара  , где
, где  - заряд на поверхности шара.
- заряд на поверхности шара.
Тогда объемная плотность энергии будет равна:
 .
.
Постоянный электрический ток
Задача 3. Сила тока в проводнике сопротивлением  равномерно растет от
равномерно растет от  до
до  за время t. Определить выделившееся в проводнике за это время количество теплоты Q. Значения R,
за время t. Определить выделившееся в проводнике за это время количество теплоты Q. Значения R,  и
и  приведены в таблице.
приведены в таблице.
| Заданные величины | номер варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
 , Ом , Ом
| 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 100 |
 , А , А
| 2 | 4 | 6 | 8 | 10 | 9 | 7 | 5 | 3 | 1 |
 , с , с
| 3 | 5 | 7 | 9 | 11 | 8 | 6 | 4 | 2 | 10 |
Решение. Согласно закону Джоуля-Ленца для бесконечно малого промежутка времени количество выделившейся теплоты будет равно:
 .
.
По условию задачи сила тока равномерно растет, т.е.  , где коэффициент пропорциональности
, где коэффициент пропорциональности  - есть величина постоянная. Тогда можно записать
- есть величина постоянная. Тогда можно записать  . Проинтегрировав последнее выражение с учетом
. Проинтегрировав последнее выражение с учетом  , найдем искомое количество теплоты:
, найдем искомое количество теплоты:
 .
.
Задача 4. Определить внутреннее сопротивление источника тока, если во внешней цепи при силе тока 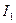 развивается мощность
развивается мощность  , а при силе тока
, а при силе тока 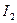 - мощность
- мощность  . Значения параметров
. Значения параметров  ,
,  ,
, 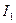 и
и 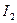 приведены в таблице.
приведены в таблице.
| Заданные величины | номер варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
 , Вт , Вт
| 10 | 15 | 12 | 8 | 5 | 18 | 13 | 3 | 7 | 6 |
 , Вт , Вт
| 13 | 20 | 18 | 11 | 9 | 27 | 16 | 7 | 12 | 10 |
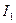 , А , А
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
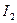 , А , А
| 3 | 5 | 8 | 6 | 9 | 11 | 15 | 14 | 13 | 18 |
Решение. Мощность, развиваемая током, вычисляется по формулам:
 и
и  , (1)
, (1)
где  и
и  - сопротивление внешней цепи. Согласно закону Ома для полной цепи:
- сопротивление внешней цепи. Согласно закону Ома для полной цепи:
 ;
;  ,
,
где  - э.д.с. источника.
- э.д.с. источника.
Решив эти два уравнения, относительно  получим:
получим:
 (2)
(2)
Выразив  и
и  из уравнений (1) и подставив в выражение (2), найдем искомое внутреннее сопротивление источника тока:
из уравнений (1) и подставив в выражение (2), найдем искомое внутреннее сопротивление источника тока:
 .
.
.
 2020-10-12
2020-10-12 111
111







