Задача 4. По двум параллельным прямым проводникам длиной 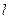 каждый, находящимся в вакууме на расстоянии
каждый, находящимся в вакууме на расстоянии 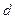 друг от друга, в противоположных направлениях текут токи
друг от друга, в противоположных направлениях текут токи 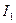 и
и 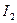 . Определить силу взаимодействия токов. Значения параметров l, d,
. Определить силу взаимодействия токов. Значения параметров l, d, 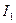 и
и 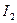 приведены в
приведены в
таблице.
| Заданные величины | номер варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, м | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
| d, см | 5 | 7 | 8 | 9 | 12 | 15 | 20 | 18 | 12 | 22 |
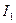 , А , А
| 10 | 22 | 3 | 40 | 35 | 60 | 30 | 28 | 19 | 50 |
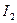 , А , А
| 30 | 25 | 8 | 66 | 29 | 110 | 15 | 44 | 33 | 30 |
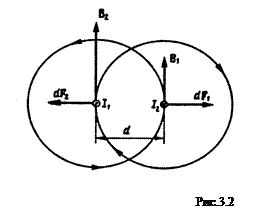
Решение. Согласно закону Ампера, на каждый элемент длины проводника 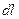 с током
с током  действует в магнитном поле, создаваемом током
действует в магнитном поле, создаваемом током 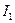 , сила
, сила
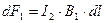 (1)
(1)
(ее направление определено по правилу векторного произведения 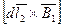 и указано на рис.3.2). Аналогичные рассуждения (ток
и указано на рис.3.2). Аналогичные рассуждения (ток 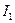 находится в магнитном поле, создаваемом током
находится в магнитном поле, создаваемом током  ) приводит к выражению:
) приводит к выражению:
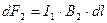 (2)
(2)
Модули магнитных индукций  и
и  определяются соотношениями:
определяются соотношениями:
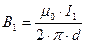 и
и 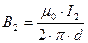 ,
,
где 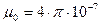 Гн/м.
Гн/м.
Подставив эти выражения в (1) и (2), получим, что сила по модулю будет определяться:
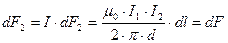 (3)
(3)
Проинтегрировав выражение (3), найдем искомую силу взаимодействия токов:
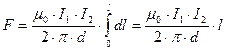 .
.
Задача 5. Катушка без сердечника (магнитная проницаемость  ) длиной
) длиной 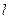 содержит
содержит 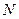 витков. По катушке течет постоянный ток I. Определить объемную плотность энергии магнитного поля
витков. По катушке течет постоянный ток I. Определить объемную плотность энергии магнитного поля  внутри катушки. Значения l,
внутри катушки. Значения l, 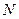 и
и 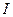 приведены в таблице.
приведены в таблице.
| Заданные величины | номер варианта | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, см | 20 | 30 | 25 | 35 | 40 | 50 | 55 | 45 | 60 | 15 |
| N | 200 | 250 | 300 | 400 | 500 | 450 | 600 | 550 | 150 | 700 |
| I, A | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 5 | 3 | 1 |
Решение. Объемная плотность энергии магнитного поля определяется выражением:
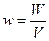 , (1)
, (1)
где 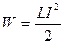 - энергия магнитного поля (
- энергия магнитного поля ( - индуктивность катушки);
- индуктивность катушки);
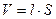 - объем катушки (
- объем катушки ( - площадь поперечного сечения катушки).
- площадь поперечного сечения катушки).
Индуктивность катушки без сердечника вычисляется по формуле:
 , (2)
, (2)
где 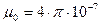 Гн/м. Подставив эти выражения в формулу (1), найдем искомую объемную плотность энергии магнитного поля внутри катушки:
Гн/м. Подставив эти выражения в формулу (1), найдем искомую объемную плотность энергии магнитного поля внутри катушки:
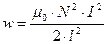 .
.
 2020-10-12
2020-10-12 100
100








