Стратегическая эквивалентность игр

Разнообразие бескоалиционных игр требует их объединения в классы эквивалентности. Каждый из классов можно исследовать на примере игры с простой структурой. Стратегическая эквивалентность является обоснованием для объединения игр в один класс, а это означает, что игры, объединенные в один класс, считаются стратегически эквивалентными.

Опр.: Пусть имеется две игры 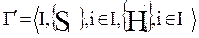и 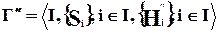. Тогда эти игры называются стратегически эквивалентными, если , при котором выполняется следующее условие:

Обычно условие стратегической эквивалентности записывают следующим образом: .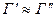

Стратегическая эквивалентность обладает следующими свойствами:

1) рефлексивность ;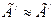

2) симметрия 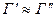и ;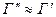

Док-во:

,

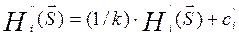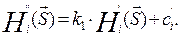
Стратегическая эквивалентность позволяет разбить все множество бескоалиционных игр на попарно непересекающиеся классы.

Различия в стратегически эквивалентных играх заключаются в масштабах выигрыша 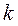и в начальном капитале 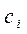. Стратегия в каждой из этих игр заключается в максимизации своего выигрыша, причем этот выигрыш максимизируется на одинаковых стратегиях.

Теорема: стратегически эквивалентные игры имеют одни и те же ситуации равновесия.

Доказательство:

Пусть имеется две стратегически эквивалентные игры: 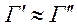. Это значит, что в ситуации равновесия должно выполняться условие:

,

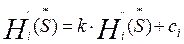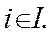
Очевидно, меняя ситуацию равновесия 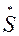на другую ситуацию 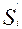, получим:

.

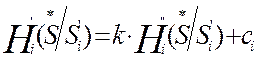Так как 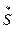— ситуация равновесия, то для игры 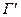должно выполнятся условие:

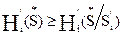, но из этого неравенства следует, что 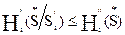, а это условие означает, что ситуация 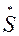есть ситуация равновесия для двух игр 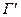и 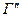, то есть две стратегически эквивалентные игры имеют одну и туже ситуацию равновесия 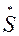. Теорема доказана.

Теорема: всякая бескоалиционная игра с постоянной суммой стратегически эквивалентна некоторой бескоалиционной игре с нулевой суммой.

Доказательство:

Рассмотрим бескоалиционную игру с постоянной суммой:

, , .

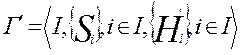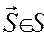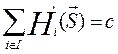Возьмем такие произвольные вещественные числа 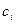, , 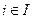чтобы 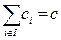. Рассмотрим функцию выигрыша 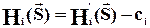. Это есть условие стратегической эквивалентности игр 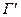и 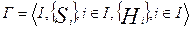(т.к. k=1, а 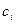не зависит от S). Тогда выигрыш игры Г равен 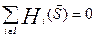. То есть игра Г является игрой с нулевой суммой. Теорема доказана.

Таким образом, мы доказали, что игры с постоянной суммой всегда можно привести к играм с нулевой суммой.