Верхняя и нижняя цены игры при использовании смешанных стратегий

Пусть 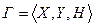— игра, а 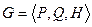— ее смешанное расширение.

Предположим, что первый игрок применяет смешанную стратегию 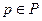. Этого игрока интересует, каков будет его гарантированный выигрыш, т.е. та наименьшая сумма выигрыша, которую он может наверняка себе обеспечить, даже если второй игрок применяет свою наилучшую смешанную стратегию .

Обозначим гарантированное значение выигрыша первого игрока при стратегии p через A(p):

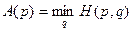Далее первого игрока будет интересовать выбор из всех возможных стратегий 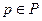такой, при которой его гарантированный выигрыш будет максимальным:

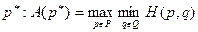Стратегия 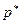называется максиминной стратегией первого игрока в смешанном расширении игры.

Для второго игрока рассуждения аналогичные. Применяя свою смешанную стратегию 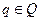, его максимальный проигрыш будет равен:

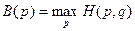Далее второго игрока будет интересовать выбор из всех возможных стратегий 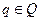такой, при которой его гарантированный проигрыш будет минимальным:

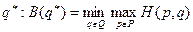Стратегия 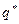является минимаксной стратегией второго игрока в смешанном расширении игры.

Таким образом, 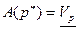называется нижней ценой игры в смешанном расширении, а 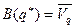называется верхней ценой игры в смешанном расширении.

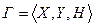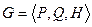Теорема. Если имеется игра , а — ее смешанное расширение, то

a) ;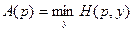

b) ;

c) ;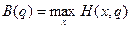

d) ;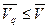

e) .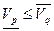

Условие «а» говорит о том, что при выборе первым игроком любой смешанной стратегии значение его гарантированного выигрыша равно значению гарантированного выигрыша при использовании вторым игроком только смешанных стратегий. Согласно условию «b» нижняя цена игры при смешанных стратегиях первого игрока не меньше нижней цены игры при чистых стратегиях, т.е. что существует смешанная стратегия, которая во всяком случае не хуже оптимальной чистой стратегии. Пункты «c»и «d» содержат аналогичные утверждения в отношении второго игрока. Пункт «e» означает, что нижняя цена игры 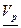при использовании смешанных стратегий не превосходит верхней цены игры 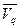, т.е. при использовании наилучших смешанных стратегий гарантированный выигрыш первого игрока не превзойдет обеспеченного проигрыша второго игрока.

Доказательство – Коршунов Ю.М. Математические основы кибернетики.

Следствие. .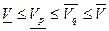

Из этого следует, что если игра Г имеет цену, т.е. 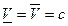(это имеет место для игр с седловой точкой), то 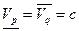, т.е. игра G также имеет цену. Поэтому оптимальная стратегия в игре Г является оптимальной и в игре G. В этом случае игру G можно не рассматривать, а оптимальные стратегии игроков находить методом, описанным для игр с седловой точкой.

Но игра G была введена для анализа таких игр, у которых 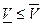. Применение смешанных стратегий позволяет найти цену игры и оптимальные стратегии игроков в этом случае.