Дележи в кооперативной игре

Решением кооперативной игры является делёж, т. е. договор о распределении выигрыша коалиции между её членами. В общем случае можно рассмотреть вектор V(I) — выигрыш коалиции и вектор дележа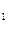 x = (x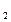, x,…,x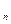), описывающий выигрыш всех участников игры. Для практической реализуемости вектор x должен удовлетворять некоторым условиям (свойствам):

1. Условие индивидуальной рациональности: x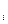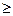V(i), i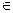I. То есть каждому игроку должен быть предложен выигрыш не меньше, чем он мог бы выиграть самостоятельно.

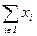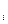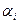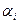
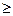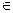2. Условие коллективной (групповой) рациональности: x(I) = = V(I), т. е. делёж реализует все потенциальные возможности данной игры. Согласно свойству индивидуальной рациональности делёж можно рассматривать в следующем виде: x= V(i) + , 0, iI, 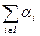= V(I) - .

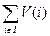Кооперативная игра, для которой свойство супераддитивности вырождается в аддитивность: V(L+K) = V(L) + V(K), K, L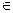I, называется несущественной. В несущественной игре имеется только один делёж, x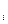= V(i).

В кооперативных играх рассматривается свойство стратегической эквивалентности.