Пространство стратегий природы

Статистических решений

Общие сведения об играх с природой или теория

В экономической практике часто приходится принимать решения при скудных априорных сведениях о протекании той или иной операции. В этих играх два игрока: 1-ый — активный игрок «статистик», 2-ой — пассивный, его выбор определяет условия протекания игры.

В результатах протекания игры второй игрок не заинтересован (он не выигрывает и не проигрывает). Таким образом, «природа» определяет всю совокупность внешних обстоятельств, которые учитываются активным игроком при выборе стратегии своего поведения.

Т. к. будущее состояние природы никогда не известно точно, то активному игроку приходится принимать решения в условиях неопределённости, но не в условиях прямого конфликта. Платой за недостаточную информированность о будущем состоянии природы является плата за ошибочное решение, которое может принять статистик. Возникает вопрос какие решения следует считать правильными, а какие — ошибочными? Каким образом можно выбрать правильное решение и отсечь неправильное?

Отсутствие сознательного противодействия со стороны природы лишь усложняет задачу выбора правильных решений. В играх с природой используются т. н. статистические решения. Соответственно, теория игр с природой называется теорией статистических решений.

Предположим, что число возможных состояний природы z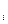конечно. Z = 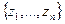— множество состояний природы. Если статистику точно известно z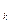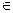Z, то будем считать его способным принять наилучшее решение в этом состоянии z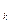. В общем случае статистику может быть известно достаточно приближенно:

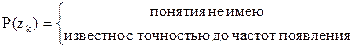
Известны частоты P’ и грубые оценки частот P’’. В каждом из этих случаев статистику приходится принимать решения, используя специфические методы теории принятия статистических решений. В первом случае надо принимать решение, которое не использует понятие вероятности состояния природы, во втором случае можно поступать двояко: можно принимать решения, используя грубые оценки частот (считая их за вероятность) или предпринять действия, позволяющие уточнить эти оценки частот. В третьем случае возникает вопрос: с помощью скольких экспериментов можно грубые оценки считать точными?

В дальнейшем вероятности состояния природы будем обозначать q(z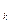). Очевидно, что состояния природы и их вероятности образуют смешанную стратегию природы. Т.е. можно считать, что множество Z = 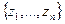и множество Q = 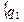,…,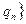образуют пространство состояний природы.