Тема 12.
Некоторые математические свойства дисперсий.
Между отдельными видами дисперсий существует взаимосвязь, которую можно записать в виде правила сложения дисперсий: Пример: Распределение сотрудников КБ по производительности труда 1. Расчет общей дисперсии
| x | f | xf | x2 | x2f |
2. Расчет дисперсии по первой группе
| x | f | xf | x2 | x2f |
3. Расчет дисперсии по второй группе
| x | f | xf | x2 | x2f |
4. Расчет межгрупповой дисперсии
| 11,2 | -2,325 | 5,405 | 135,140 | |
| 17,4 | 3,875 | 15,015 | 225,234 | |
| 360,375 |
5. Расчет средней из индивидуальных дисперсий.
Эмпирическое корреляционное отношение (ЭКО). На основании правила сложения дисперсий вычисляется эмпирическое корреляционное отношение (ЭКО), которое равно квадратному корню из отношения межгрупповой дисперсии к общей:
Такой порядок вычисления обусловлен разложением общей вариации на вариацию, зависящую от фактора, положенного в основу группировки (в нашем примере – повышение и неповышение квалификации), которая численно равна межгрупповой дисперсии, и общую вариацию.
Межгрупповая дисперсия составляет часть общей дисперсии и складывается под влиянием только одного группировочного фактора. Именно поэтому подкоренное выражение показывает долю вариации за счет группировочного признака.
ЭКО изменяется в переделах от нуля до единицы. Чем ближе его значение к единице, тем большая доля вариации падает на группировочный признак.
1. При вычитании из всех значений признака некоторой постоянной величины дисперсия не изменится.
2. При сокращении всех значений на постоянный множитель дисперсия уменьшится в раз.
3. Средний квадрат отклонений значений признака от постоянной произвольной величины больше дисперсии признака на квадрат разности между средней арифметической и постоянной величиной.
На основании свойств дисперсии ее можно подсчитать способом отсчета от условного нуля и способом моментов.
| Интервал | ||||||||
| 90-100 | -30 | -3 | -6 | |||||
| 100-110 | -20 | -2 | -12 | |||||
| 110-120 | -10 | -1 | -8 | |||||
| 120-130 | 2 250 | |||||||
| 130-140 | ||||||||
| 140-150 | ||||||||
| 150-160 | ||||||||
| 160-170 | ||||||||
| 170-180 | ||||||||
| 6 390 |
В аналитической группировке рассчитывают несколько видов дисперсии, которые определяют характер вариации и взаимосвязи признаков:
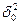 - это общая дисперсия;
- это общая дисперсия;
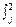 - Внутригрупповая дисперсия;
- Внутригрупповая дисперсия;
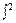 - Средняя из внутригрупповых дисперсий;
- Средняя из внутригрупповых дисперсий;
Рассмотрим показатели дисперсии в структурной группировке.
1. Общая дисперсия
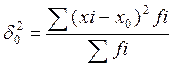
Общая дисперсия зависит от случайных и не случайных факторов определяющих вариацию признака, т.е. содержит детерминированную и стохастическую компоненту вариации и взаимосвязи.
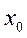 − общая средняя;
− общая средняя; 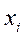 − вариант признака;
− вариант признака; 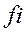 − вес вариантов.
− вес вариантов.
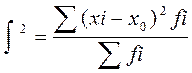
Этот показатель, который определяет детерминированную компоненту вариации и функциональную составляющую взаимосвязи.
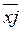 − средние по группе;
− средние по группе;
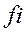 − вес группы в составе совокупности.
− вес группы в составе совокупности.
3. Внутригрупповая дисперсия
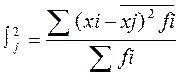
Определяет случайную составляющую вариации и стохастическую компоненту взаимосвязи.
4. Среднее из внутригрупповых дисперсий
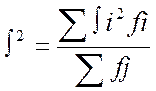
Характеризует стохастическую компоненту вариации и взаимосвязи по совокупности в целом. Таким образом, общая дисперсия определяется суммой средних из внутригрупповых и межгрупповых дисперсий.
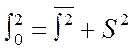
5. Долю межгрупповой дисперсии определяет коэффициент детерминации, значения которого находятся в пределах от 1 до 0.
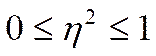
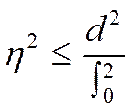
Значение коэффициента = 0 характеризует наличие только стохастической причины вариации и отсутствие взаимосвязи между признаками.
Значения коэффициента равно 1 характеризует детерминированную причину вариации признака и стохастическую составляющую взаимосвязи.
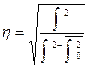
Часто используются для оценки силы связи между признаками существует качественная взаимосвязь, определяющаяся по формуле Чеддока, которая имеет вид.
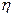 | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Сила связи | Слабая | Умеренная | Заметная | Сильная | Тесная |
Меру линейной связи отражает коэффициент линейной корреляции между величинами х и у.
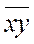 - среднее от производной
- среднее от производной
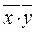 - произведение средних
- произведение средних
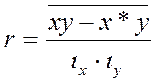
Квадрат линейного коэффициента корреляции называют линейным коэффициентом детерминации. Сопоставляя коэффициенты детерминации с линейным коэффициентом детерминации можно определить степень близости и отличия существующей связи от линейной.
Существуют другие способы определения силы и направления связи, которые основаны на построении ранжированных рядов.
-1≤r≤1
Коэффициенты ранговой корреляции так же как и корреляционные отношения могут определить направление и силу взаимосвязи. Так, например, линейных коэффициент корреляции, значения которого находятся в пределах от -1 до 1. Значения коэффициента равные 1, характеризуют прямопропорциональную линейную функциональную связь между величинами х и у.
Значения коэффициента r=0 свидетельствует об отсутствии связи, при r= -1 связь линейная обратнопропорциональная однозначно определенная.
7. Коэффициент корреляции рангов.
Коэффициенты корреляции рангов могут определить силу и направление взаимосвязи как между числовыми, так и между атрибутивными признаками (включая сопоставление между числовыми и атрибутивными признаками), при условии, что единицы совокупности были упорядочены по сопоставленным признакам и пронумерованы, т.е. проранжированы.
Существует коэффициент корреляции рангов Спирмена.
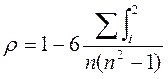
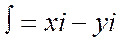
Коэффициент корреляции ранга Кендела
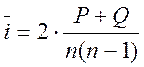
При определении величины Р подсчитывается количество чисел, находящихся справа от каждого из элементов рангов, прегрешения у которых имеет величину ранга, превышающего ранг рассматриваемого элемента.
величину Q – рассчитывают путем сложения числа единиц с совпадающими рангами коэффициента ранговой корреляции Кендела, находится в пределах от 1 до 1 и равно 0 при отсутствии связи -1≤ ≥1 между признаками.
Ранговые методы позволяют определить степень связи между несколькими признаками.
Коэффициент определяется по формуле:
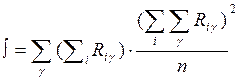
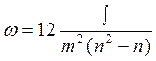
m – число факторов
n – количество регулируемых величин
Ry – ранг i-го фактора j
 2014-02-04
2014-02-04 939
939

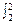 -
- 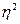 -
- 






