РЕШЕНИЕ ЗЛП С ПОМОЩЬЮ EXCEL
L(x) = 130,5x1 +20х2 +56х3 +87,8х4 ®mах;
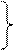 -1,8х1 +2x2 + х3 -4х4 =756
-1,8х1 +2x2 + х3 -4х4 =756
- 6х1 +2x2 + 4хз - х4 ³ 450
4х1 - 1,5х2 + 10,4х3 + 13х4 £ 89
Введем значения из математической модели в экранную форму
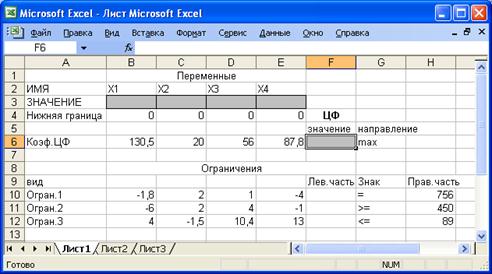
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано.
=СУММПРОИЗВ(В$3:Е$3;В6:Е6),
| Левая часть ограничения | Формула Excel |
| -l,8x1 +2x2 +x3 - 4х4 или BIO* B3 + С10*СЗ+ D10*D3 + E10*E3 | =СУММПРОИЗВ(В$3:Е$3;В10:Е10) |
| -6x1 +2x2 +4х3 -x4 или В11* ВЗ + СП*СЗ + D11*D3 +E11*E3 | =СУММПРОИЗВ(В$3:Е$3;В11:Е11) |
| 4x1 – 1,5х2 +10,4х3 +13x4 или В12*ВЗ+ С12*СЗ+D12*D3 + E12*E3 | =СУММПРОИЗВ(В$3:Е$3;В12:Е12) |
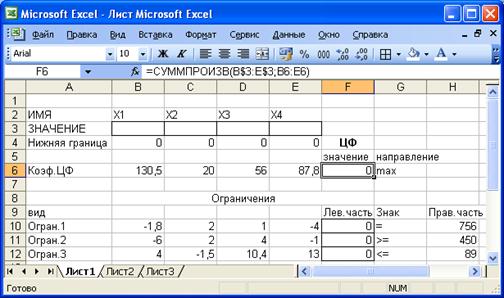
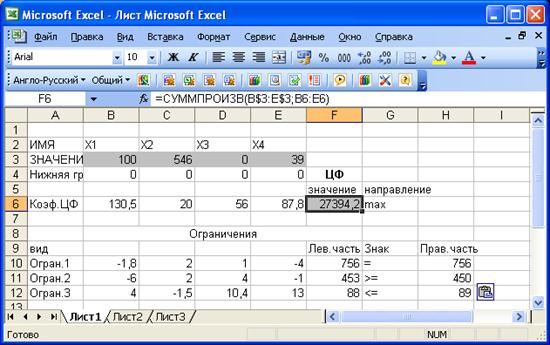
Экранная форма задачи после ввода всех необходимых формул
(курсор в ячейке F6)
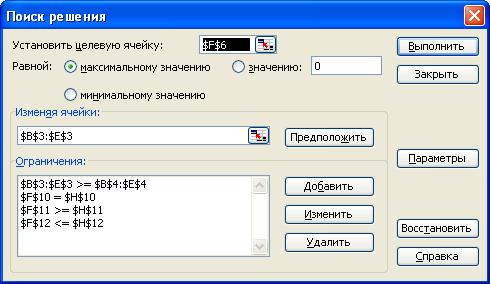
Дальнейшие действия производятся в окне "Поиск решения", которое вызывается из меню "Сервис"
"Добавление ограничения"
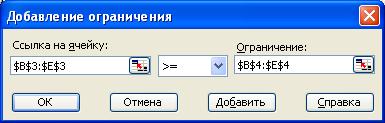 Нажмите кнопку "Добавить", после чего появится окно
Нажмите кнопку "Добавить", после чего появится окно
•
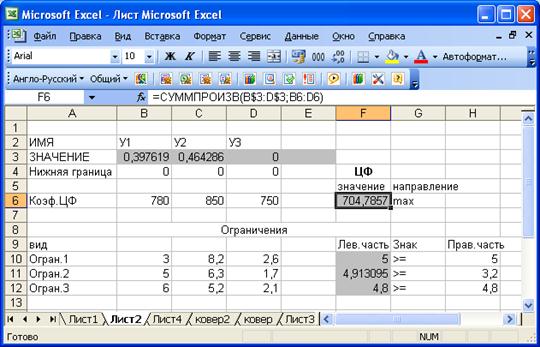
Окно "Поиск решения" после ввода всех необходимых данных задачи представлено на рис.
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".
ДВОЙСТВЕННАЯ ЗАДАЧА.
В 1975 году наш соотечественник Леонид Витальевич Канторович был удостоен Нобелевской премии по экономике за разработку теории оптимального использования ресурсов.
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряжённой по отношению к прямой (исходной). Теория двойственности полезна для проведения качественных исследований ЗЛП.
Переменные двойственной задачи yi называются двойственными оценками, «ценами» ресурсов, теневыми ценами.
Каждая задача двойственной пары фактически является самостоятельной ЗЛП и может быть решена независимо от другой.
Пример.
Цех выпускает три вида обувных картонов.
Производственные возможности цеха:
a. Суточный фонд рабочего времени оборудования – 780 ч,
b. Суточный расход сырья – 850 т,
c. Суточный расход электроэнергии – 750 кВт/ч
Нормы расхода производственных ресурсов на единицу различных видов картона представлены в таблице:
| Ресурсы | Норма затрат на единицу продукции | ||
| Оборудование, ч | |||
| Сырьё, т | 8,2 | 6,3 | 5,2 |
| Электроэнергия, кВт/ч | 2,6 | 1,7 | 2,1 |
Прибыль от реализации 1т картона составляют: 1-го вида – 5руб., 2-го вида – 3,2 руб., 3-го вида – 4,8 руб.
Составить модель задачи плана производства продукции, обеспечивающего максимальную прибыль.
L(x)=5х1+3,2х2+4,8х3®max
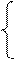 3х1+5х2 + 6х3 £780
3х1+5х2 + 6х3 £780
8,2х1+6,3х2+5,2х3£850
 2,6х1+1,7х2+2,1х3£750
2,6х1+1,7х2+2,1х3£750
L max=705 при х1=31,07, х2=0 и х3= 114,5
Составляем двойственную задачу:
S(у)=780у1+850у2+750у3 ®min
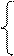 3у1+8,2у2+2,6у3³5
3у1+8,2у2+2,6у3³5
5у1+6,3у2+1,7у3³3,2
6у1+5,2у2+2,1у3³4,8
Обе задачи обладают следующими свойствами:
1. В одной задаче ищут максимум линейной функции, в другой - минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в стандартной форме, причём в задаче максимизации – все неравенства вида «≤», а в задаче минимизации – все неравенства вида «≥».
4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
Для задачи I А=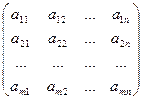 , для задачи II А=
, для задачи II А=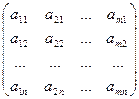
Т.е. левая часть ограничений определяет стоимость ресурсов, затраченных на производство единицы продукции.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.
Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимодвойственными задачами.
| Общая модель ЗЛП | |
| Исходной (прямой) | Двойственной |
L(x) = 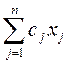 ®max при ограничениях ®max при ограничениях 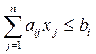 (i = 1, 2,……,m) x j³ 0; j=1,2,….,n (i = 1, 2,……,m) x j³ 0; j=1,2,….,n | S(y)=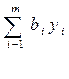 ® min ® min 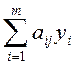 ³ сj yi³ 0 ³ сj yi³ 0 |
Первая (основная) теорема двойственности.
Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причём оптимальные значения их линейных функций равны:
Fmax=Smin или F(X*) =S(Y*)
Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану X*=(x , x
, x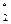 ,…, x
,…, x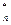 ) и получать максимальную прибыль Fmax либо продавать ресурсы по оптимальным ценам У*=(у
) и получать максимальную прибыль Fmax либо продавать ресурсы по оптимальным ценам У*=(у , у
, у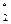 ,…, у
,…, у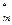 ) и возместить от продажи равные ей минимальные затраты на ресурсы Zmin.
) и возместить от продажи равные ей минимальные затраты на ресурсы Zmin.
Вторая теорема двойственности (теорема о дополняющей нежесткости)
Пусть X=(x1, x2,…, xn) - допустимое решение прямой задачи, а У=(у1 у2…, уm) - допустимое значение двойственной задачи. Для того, чтобы они были оптимальными решениями соответственно прямой и двойственной задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
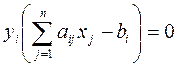

Эти условия позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.
Цель?
1. Продать ресурсы.
2. Оценка дефицитности ресурса.
Если «у» = 0, то этот ресурс недефицитный (не из-за того, что его запас неограничен, а от того, что его невозможно использовать полностью в оптимальном плане)
3. Определение ценности ресурса.
• Чем больше «у», тем острее дефицитность ресурса и поэтому выгодно увеличивать именно его для увеличения прибыли.
• Ценность различных видов ресурсов нельзя приравнивать к действительным ценам. Речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность ресурса только относительно полученного оптимального решения.
Двойственные задачи могут быть также несимметричные (= в ограничениях прямой задаче) и смешанными (=, ³,£)
ТРАНСПОРТНАЯ ЗАДАЧА.
Для моделирования транспортно-производственных систем используется задачи линейного программирования, а именно транспортные задачи (распределительные).
Применяется при закреплении ресурсов по видам работ, при закреплении транспортных средств за маршрутами, при составлении топливно-энергетических балансов, при распределении заказов между фирмами, при распределении выпуска продукции по видам оборудования и т.д.
Общая формулировка задачи имеет следующий вид: пусть осуществляется производство некоторого товара в пунктах m. Объем производства товара в каждом пункте равен соответственно a1,a2,…,am. Товар необходимо доставить в магазины или потребителям, находящимся в других населенных пунктах n. Известна потребность каждого потребителя в товаре: b1,b2,…,bn. Задана также стоимость cij транспортировки товара из каждого пункта производства Ai каждому потребителю Bj. Требуется составить план завоза товара в магазины, обеспечивающий удовлетворение их спроса при минимальных транспортных издержках.
Дано:
Ai – множество наименований поставщиков;
m – общее количество поставщиков;
Bj – множество наименований потребителей;
n – общее количество потребителей;
ai - объем произведенной продукции в i -ом пункте;
bj - спрос на продукцию в j-ом пункте;
Cij – тариф (стоимость, затраты) на транспортировку единицы продукции от i-го поставщика j-му потребителю.
Требуется найти такие объемы транспортировки продукции от каждого поставщика к каждому потребителю (xi,j > 0), при которых достигается минимум транспортных затрат (что при фиксированных ценах реализации продукции равносильно максимизации прибыли), то есть:
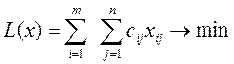
При этом должны соблюдаться условия ограничения:
- полное удовлетворение спроса во всех пунктах потребления
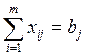 , j= 1, 2….n
, j= 1, 2….n
- полный вывоз продукции от всех поставщиков
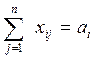 , i=1,2…m
, i=1,2…m
xij ³ 0
необходимым и достаточным условием разрешимости задачи является условие баланса:
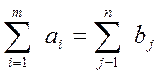
Т.е. сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления.
Такая задача называется закрытой и может быть решена многими способами: симплексным методом, методом потенциалов, метод северо-западного угла, метод минимальной стоимости и т.д.
Наглядной формой представления модели ТЗ является транспортная матрица:
| Пункты отправления, Ai | Пункты потребления, Bj | Запасы (ед.прод.) | ||||||
| B1 | B2 | … | Bn | |||||
| A1 | C11 | C12 | … | C1n | a 1 | |||
| X11 | X12 | X1n | ||||||
| A2 | C21 | C22 | … | C2n | a 2 | |||
| X21 | X22 | X2n | ||||||
| … | … | … | … | … | … | |||
| Am | Cm1 | Cm2 | … | Cmn | am | |||
| Xm1 | Xm2 | Xmn | ||||||
| Потребность (ед.прод.) | b 1 | b2 | … | bn |  |
Пример.
Исходные данные.
| 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. | |
| 1-й склад | ||||
| 2-й склад | ||||
| 3-й склад | ||||
| 4-й склад | ||||
| Потребности, шт. |
Целевая функция и ограничения данной задачи имеют вид
L(X)= 2х11 +9x12 +7x13 +х21 +5х23 +5x31 + 4x32 +100хзз +2x41 +3x42 +6x43 ®min;
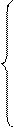 Х11 +Х12 +Х13 =25
Х11 +Х12 +Х13 =25
X21+X22+X23=50,
Х31 + Х32+ Х33 =35
Х41 + Х42 + X43 =75,
Х11+Х21+Х31=45,
Х12 + Х22 + Х32 =9О
Х13 + Х23 + Х33 =5О
хij ³ 0; xij- целые (i = 1…4; j = l..3).
1. Метод северо-западного угла.
| 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. | |
| 1-й склад | ||||
| 2-й склад | ||||
| 3-й склад | ||||
| 4-й склад | ||||
| Потребности, шт. |
Северо-западный угол таблицы – это её левый верхний угол, то есть клетка в 1-й строке и 1-м столбце – клетка (1, 1).
Поэтому рассмотрим 1-го поставщика и 1-го потребителя: у поставщика есть 25 единиц груза, а потребителю нужно 45 – ставим всю сумму. Так как поставщик А 1 израсходовал все свои 25 единиц груза, то мы исключаем его из рассмотрения (первая строка больше не рассматривается).
Северо-западный угол нижней таблицы – это клетка (2,1). Поэтому рассмотрим 2-го поставщика и 1-го потребителя. Мощность поставщика А2 равна 50 единиц, а оставшийся спрос потребителя В1 равен 20 (45-25). Записываем 20 в клетку (2,1). Потребителю В1 полностью удовлетворен спрос и поэтому остальные клетки 1-го столбца исключаем из рассмотрения.
Таким способом рассматриваем всех поставщиков и потребителей, исключая из рассмотрения после очередного шага либо строку, либо столбец.
В результате получаем следующую таблицу.
| 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. | |
| 1-й склад | - | - | ||
| 2-й склад | - | |||
| 3-й склад | - | - | ||
| 4-й склад | - | |||
| Потребности, шт. |
Для полностью заполненной таблицы должно соблюдаться следующее соотношение: число заполненных клеток = число строк + число столбцов – 1. если это соотношение не выполняется, то возникает особый случай.
Подсчитаем суммарные затраты.
25*2+20*1+30*0+35*4+25*3+50*6= 585
2. Метод «минимальных тарифов».
| 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. | ||||
| 1-й склад | |||||||
| 2-й склад | |||||||
| 3-й склад | |||||||
| 4-й склад | |||||||
| Потребности, шт. |
На каждом шаге нужно делать поставку в клетку с наименьшей стоимостью перевозки единицы среди всех заполненных клеток.
Среди всех незаполненных клеток у клетки (2,2) наименьшая стоимость перевозки – 0, поэтому делаем поставку в эту клетку – 50 (исключаем вторую строчку, как полностью использованную).
Среди незаполненных клеток наименьшая стоимость перевозки единицы груза – 2 у клеток (1,1) и (1,4). Выбираем ту клетку, куда можно сделать наибольшую поставку.
И так далее. Окончательный вариант.
| 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. | ||||
| 1-й склад | |||||||
| 2-й склад | |||||||
| 3-й склад | |||||||
| 4-й склад | |||||||
| Потребности, шт. |
Подсчитаем суммарные затраты.
25*2+20*2+50*0+35*4+5*3+50*6= 545
Как видно, при учитывании стоимости перевозки, общая сумма затрат уменьшается.
Метод «минимальных тарифов» можно проводить по строкам или столбцам.
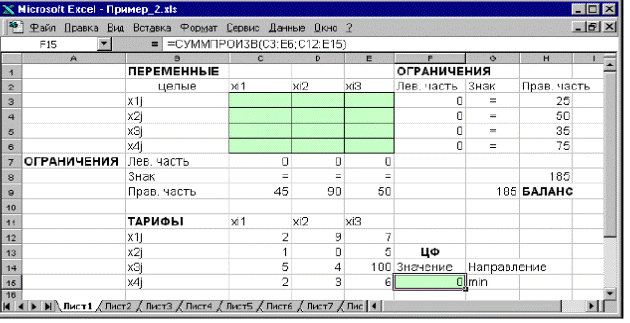 3. С помощью Excel
3. С помощью Excel
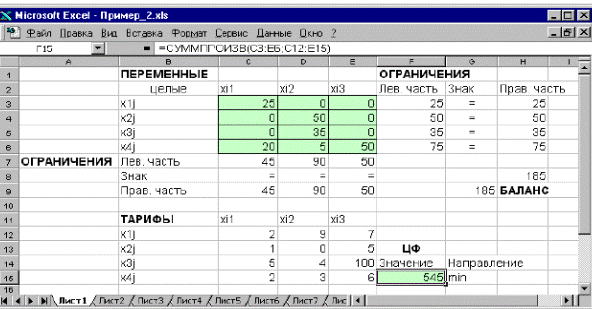
Экранная форма задачи (курсор в целевой ячейке F 15)
Формулы экранной формы задачи.

Ограничения и граничные условия задачи.
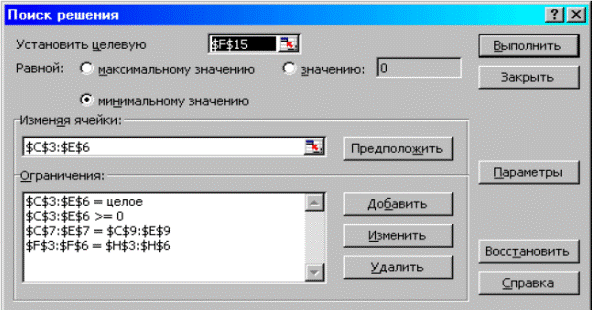
Экранная форма после получения решения задачи.
ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ.
Результат экономической деятельности предприятий и их подразделений характеризуется множеством параметров, связи которых с результативным признаком и между собой обычно неизвестны.
Корреляционные и регрессионные модели дают возможность с достаточной полнотой установить эти связи, на основе которых становится возможным управлять производством с научных позиций.
Корреляционно-регрессионные модели относятся к методам эконометрики (раздел ЭММ, который посвящен построению математических моделей в основе которых лежит статистика и теория вероятности).
Два разных анализа.
Первоначально термин «регрессия» был употреблен Ф.Гальтоном (1886) в теории наследственности, затем его теоретические основы были разработаны К.Пирсоном, Р.Фишером, М.Бартлеттом и др. Значительным вкладом в анализ явилась разработка метода наименьших квадратов К.Гауссом, А.Лежандром, А.Марковым и А.Колмогоровым.
Регрессия – линия или вид зависимости одной случайной величины или нескольких величин.
Регрессионный анализ - определение аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков.
Задачи регрессионного анализа – оценка функциональной зависимости (прямая, обратная) и расчет параметров математической зависимости.
Корреляция – статистическая зависимость между случайными величинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Корреляция – соответствие, взаимосвязь.
Корреляция бывает:
• Парная (связь между двумя признаками: результативным и факторным или двумя факторными)
• Частная (зависимость между результативным и одним факторным признаком или двумя факторными признаками при фиксированном значении других факторных признаков)
• Множественная (зависимость между результативным признаком и двумя и более факторными, включенными в исследование)
Корреляционный анализ- позволяет определить количественную зависимость результативного признака от изучаемых факторов.
Задачи корреляционного анализа – оценить тесноту связи и достоверность (значимость) полученной модели и возможность её использования для всей генеральной совокупности (не только, что рассчитывали, но и для других предприятий). Позволяет определить количественную зависимость результативного признака от изучаемых факторов.
Задача корреляционно-регрессионного анализа – определить общий вид математической модели в виде уравнения регрессии, рассчитать статистические оценки неизвестных параметров, входящих в это уравнение, и проверить статистические гипотезы о зависимости функции от её аргументов.
Пример.
Необходимо определить вид корреляционно-регрессивной зависимости и её достоверность по следующим данным.
По 10 однотипным предприятиям имеются следующие данные по выпуску продукции в тыс. единиц и о расходе топлива в тоннах.
Фактор или аргумент – выпуск (х).
Функция (результат)– расход топлива (у).
| х | у | х2 | ху | 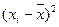 | 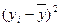 | |
| 56,25 | ||||||
| 42,25 | ||||||
| 20,25 | ||||||
| 20,25 | ||||||
| 6,25 | ||||||
| 6,25 | ||||||
| 2,25 | ||||||
| 56,25 | ||||||
| 56,25 | ||||||
| 132,25 | ||||||
| å | 398,5 |
1 этап – определение формы связи между х и у и выбор математической модели

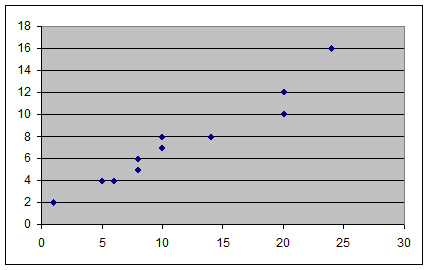
Для этого строится поле корреляции в виде графика. Область, ограничивающая точки – корреляционное облако. Чем плотнее точки, тем теснее связь.
Уравнение регрессии или модель связи составляется на основе характера связи между функцией и аргументом.
Требования к построению уравнения регрессии:
• Совокупность исходных данных должна быть однородной и математически описываться непрерывными функциями
• Наличие достаточно большого объема исследуемой выборочной совокупности (25 и больше)
• Причинно-следственные связи между явлениями и процессами, по возможности, следует описывать линейной (или приводимой к линейной) формой зависимости
• Количественное выражение факторных признаков
• Постоянство территориальной и временной структуры изучаемой совокупности
Форма связи может быть выражена как линейной функцией (уравнение прямой) так и нелинейными функциями (полиномы разных порядков, гипербола, степенная функция и др.)
Подбор функции для выражения формы связи между признаками проходит несколько этапов: графический, логический, экономический, математический и т.д.
Вначале рассматривается линейная форма связи, так как такая форма связи часто встречается на практике и для неё разработан хороший математический аппарат.
Полученный график показывает, есть ли какая то зависимость: у нас близко к линейной зависимости, которую можно выразить уравнением прямой (парная регрессия: характеризует связь между двумя признаками)
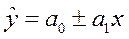
а0 -свободный коэффициент, не имеет экономического смысла и показывает значение результативного признака у, если факторный признак х =0
а1 - коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак у, если переменную х увеличить на единицу измерения.
Знак показывает направление связи: > 0-связь прямая; при < 0 – связь обратная
2 этап.
Расчет параметров уравнения регрессии с помощью метода наименьших квадратов (квадрат отклонений от прямой линии).
Для нахождения параметров а0 и а1 необходимо решить следующую систему нормальных уравнений
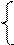 n a0 + a1 S x = S y
n a0 + a1 S x = S y
a0 S x + a1 S x2 = S xy
n – количество наблюдений
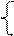 10 a0 + a1 125 = 80
10 a0 + a1 125 = 80
a0 125 + a1 1961 = 1218

 А. Метод определителей
А. Метод определителей

 10 125 = 10*1961-1252=3985
10 125 = 10*1961-1252=3985
 125 1961
125 1961
 а0 =
а0 = 
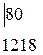
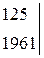 =4630 а0 =4630/3985=1,16
=4630 а0 =4630/3985=1,16
 а1 =10*1218-125*80=2180 а1 =2180/3985=0,547
а1 =10*1218-125*80=2180 а1 =2180/3985=0,547
Б. Формулы.
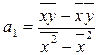
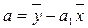
а1 =121.8-12,5*8/196,1-12,52=0,547
а = 8-0,547*12,5=1,16
В. Метод подставки.
а0= (80- 125 а1)/10=8-12.5 a1
(8- 12.5 а1)*125+1961 a1 =1218
a1 =1218-8*125/1961-125*12.5=0.547
а0= 8-12.5*0,547=0,1625
Подставляем вычисленные коэффициенты в уравнение линейной регрессии
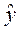 = 1,16 + 0,547 х
= 1,16 + 0,547 х
если (-), то связь обратная.
Нужно построить на поле корреляции прямую (например, х=0 и х=10) и посмотреть, на сколько линия вписывается в поле корреляции: если близко, то правильно рассчитали (может получиться так, что применение регрессионного анализа вообще проблематично).
Нашли зависимость, но нам важно знать, можно ли распространить её на другие предприятия.
3 этап.
Оценим тесноту связи (близость исследуемой формы связи к линейной) с помощью коэффициента парной корреляции.
КПК характеризует тесноту и вид зависимости между х и у и обозначается rxy или r.
-1 £ r £ 1
Положительное значение коэффициента свидетельствует о наличии прямой связи, отрицательное – обратной.
Чем ближе значение r по абсолютному значению к 1, тем теснее связь между х и у. Принято, что при «от ±0,7 до ±1,0» связь сильная, «от ±0,5 до ±0,7» - умеренная, «от ±0,3 до ± 0,5» - слабая, «от 0 до ± 0,3» - практически отсутствует.
Если = 1, то пропорционально жесткая связь (линейная, функциональная), но в реальной жизни очень редко (например путь и время из дома на работу: разное, хотя путь один).
Если близко к 0, то связь очень слабая или отсутствует.
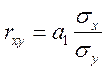
s - средне-квадратичное отклонение случайных величин.
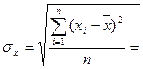 6,31
6,31 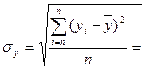 3,6
3,6
rxy = 0,547*6.31/3.6=0.96
По значению коэффициента видно, что связь тесная, прямая, модель неплохая.
Можно также рассчитать по формуле.
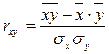
4 этап.
Вычисляем «коэффициент эластичности» - «Э», который показывает, на сколько процентов изменится результативный признак «у» при изменении факторного признака «х» на 1%.
Э = а1 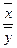
Э = 0,547*12,5/8=0,85
Полученное значение говорит о том, что если х изменится на 1%, то у изменится на 0,85%.
5 этап
Часто на практике для оценки тесноты линейной связи между исследуемыми величинами, т.е. меры адекватности регрессионной модели статистическим данным, используют коэффициент детерминации. Показывает, какая доля вариации переменной у учтена в модели и обусловлена влиянием на нее переменной х.
Чем больше это значение, тем выше степень адекватности уравнения регрессии полученное опытным путем.
R2= r2 *100%
R2= 0,962 *100% = 92.16%
Полученное значение показывает, что расход топлива на 92% зависит от объема производства. Не учтено 8%, т.е. есть другие факторы, которые влияют на результат.
6 этап
Для оценки значимости коэффициента корреляции используют t-критерий Стьюдента, который показывает:
• на сколько значима полученная по данной выборке модель (действительно ли между факторами имеется корреляционная связь или отличие КК от нуля связано со случайной ошибкой эксперимента)
• какой процент отклонений возможен при её использовании для всей генеральной совокупности (других объектов).
Расчетные значения можно определить по формуле:
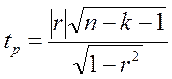
k – число факторных признаков, включенных в модель (у нас -1)
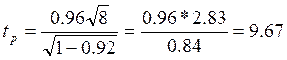
Полученное уравнение считается достаточно значимым, если tp ³ tТ, принятому при определенном уровне значимости.Табличное значение берется из специальной таблицы «Критические значения t-критерия Стьюдента на уровне значимости 0,1; 0,05;0,01». Столбец 0,1 говорит о том, вероятность значимости равна 90%, т.е. 10% ошибка. Чаще всего сравнивают с a=0,05 и «число средней свободы» = n-2.
В нашем случае tТ= 2,31, т.е. tp ³ tТ и это говорит о том, что модель хорошая.
7 этап
Для проверки значимости уравнения регрессии в целом используют F-критерий Фишера.
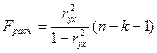
Fрасч= (0,962/1- 0,962) * (10-1-1)=92
Табличное значение при числе степеней свободы 1 и 8 и уровне значимости 0,05 равно 5,32, т.е. фактическое значение превышает табличное, можно сделать вывод, что уравнение статически значимо.
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ.
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости переменной у от нескольких факторов х1,х2,…….,хk которая может быть решена с помощью множественного корреляционно-регрессионного анализа.
Чаще всего используется уравнение линейной множественной регрессии
yx=a0+a1x1+a2x2+……+akxk
Прежде чем строить ММ, необходимо отобрать наиболее существенные факторы, используя КПК. Предпочтение отдается тому фактору, который более тесно, чем другие факторы, связан с результативными признаками. Важно, чтобы связь х с у была больше, чем между факторами х
Наиболее достоверные результаты можно получить, когда число объектов наблюдения (n) превышает число анализируемых признаков в 6-8 раз.
Методы:
1. Сравнение значений ЛКК
2. Метод включения факторов по одному пошагово, начиная с наибольшего КК.
3. Метод исключения факторов до тех пор, пока модель не станет удовлетворять определенным условиям.
Пример:
Требуется провести отбор факторов в модель множественной линейной регрессии на основе условных исходных данных.
| № организации | Объем реализации продукции, млн руб (У) | Расходы на рекламу, тыс. руб. (Х1) | Цена единицы продукции, руб. (Х2) | Отдел маркетинга в организации (1-есть, 0-нет)(Х3) |
| 1,27 | ||||
| 1,34 | ||||
| 1,25 | ||||
| 1,28 | ||||
| 1,43 | ||||
| 1,25 | ||||
| 1,53 | ||||
| 1,57 | ||||
| 1,27 | ||||
| 1,46 | ||||
| 1,28 | ||||
| 1,55 | ||||
| 1,35 | ||||
| 1,49 | ||||
| 1,46 | ||||
| 1,25 | ||||
| 1,29 | ||||
| 1,28 | ||||
| 1,33 | ||||
| 1,51 |
| У | Х1 | Х2 | Х3 | |
| У | ||||
| Х1 | -0,30497 | |||
| Х2 | 0,727375 | 0,051692 | ||
| Х3 | 0,178518 | 0,287196 | 0,295063 |
На первом этапе включим в модель все факторы и воспользуемся методом исключения факторов.
1. Для проведения корреляционного анализа воспользуемся программой «Анализ данных», инструмент «Корреляция»
В результате получаем
Анализ полученных коэффициентов парной корреляции показывает, что слабая связь между У и Х3
2. Построим модель зависимости. Воспользуемся программой «Анализ данных», инструмент «Регрессия»
 2014-02-02
2014-02-02 1388
1388
