Задачи
6.1. Сколько имеется абстрактных графов с 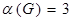 , имеющих гамильтонов цикл
, имеющих гамильтонов цикл
а) с 5 вершинами; б) с 6 вершинами?
6.2. Чему равно число вершинного покрытия графа 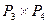 ?
?
6.3. Найдите 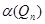 ,
, 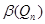 ,
, 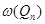 .
.
6.4. Сколько наибольших независимых множеств имеется у графа а) 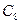 ; б)
; б) 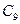 ; в)
; в) 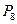 ;
;
г) 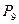 ?
?
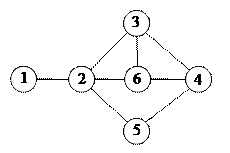
6.5. Найдите наибольшее независимое множество с помощью дерева решений в графе,
показанном на рисунке.
6.7. Сколько листьев будет в дереве вариантов для независимых множеств, построенном
для графа 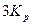 ?
?
6.8. Рассмотрим две эвристики для задачи о независимом множестве:
1) выбирать вершину наибольшей степени и удалять ее, пока не останется
независимое множество;
2) выбирать вершину наименьшей степени и удалять ее окрестность, пока не
останется независимое множество.
Какая из них всегда дает правильный ответ а) для графа 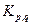 ; б) для графа
; б) для графа 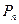 ; в) для графа
; в) для графа 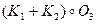 ?
?
6.9. Найдите наименьшее вершинное покрытие алгебраическим методом в графе,
показанном на рисунке. Примените к нему также приближенный алгоритм.

6.10. Даны графы 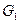 ,
, 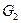 и
и 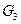 , с 9 вершинами каждый. Известно, что
, с 9 вершинами каждый. Известно, что 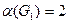 ,
,
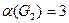 ,
, 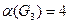 . Чему равно
. Чему равно
1) 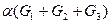 ;
;
2) 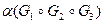 ;
;
3) 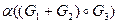 ;
;
4) 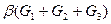 ;
;
5) 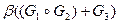 ?
?
 2014-02-04
2014-02-04 528
528








