ГЛАВА 8 ЗАДАЧА АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ РЕГУЛЯТОРОВ
После определения закона оптимального управления следующим шагом является выбор структуры управляющих устройств и их параметров, т.е. синтез автоматических систем. При синтезе автоматических систем может быть задана или не задана структура или некоторая часть структуры управляющего устройства. Соответственно, задача синтеза заключается в определении параметров и структуры управляющих устройств при необходимости. Первоначально, синтез автоматических систем осуществлялся проектировщиками без каких-то общих формальных правил на основе опыта и инженерной интуиции. При этом достаточно редко удавалось настроить автоматические системы на оптимальный режим.
Впервые в СССР единые формальные правила для синтеза оптимальных автоматических систем разработал А.М. Летов. Соответствующий подход назван аналитическим конструированием регуляторов (АКР). За рубежом аналогичные основополагающие работы связаны с именем Калмана.
Под аналитическим конструированием регуляторов (АКР) понимают проблему аналитического нахождения алгоритма работы управляющего устройства замкнутой системы, обеспечивающего наилучшее качество системы (на основании общих формальных правил) за счёт определения критерия качества, описываемого функционалом, который физически характеризует точность работы системы и энергетические затраты на управление.
Существует достаточно большое количество задач АКР. Рассмотрим некоторые наиболее простые примеры.
Пример 1. Пусть линейный нестационарный объект описывается уравнениями состояния
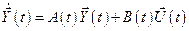 ; (8.1)
; (8.1)
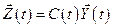 , (8.2)
, (8.2)
где 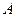 ,
, 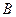 ,
, 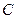 - матрицы размером
- матрицы размером 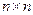 ,
, 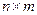 и
и 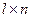 соответственно;
соответственно;
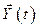 ,
,  и
и 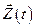 -
- 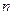 -,
-, 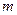 - и
- и 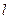 -мерные векторы состояния, управления и выхода соответственно.
-мерные векторы состояния, управления и выхода соответственно.
Пусть задан желаемый выходной вектор 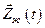 . Необходимо при минимальных затратах на управление
. Необходимо при минимальных затратах на управление  получить реальный выходной сигнал
получить реальный выходной сигнал 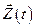 , близкий к желаемому
, близкий к желаемому 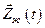 . Другими словами, главными условиями в таких задачах являются не только совпадение реальных выходных параметров
. Другими словами, главными условиями в таких задачах являются не только совпадение реальных выходных параметров 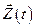 с желаемыми
с желаемыми 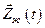 , но и минимальность затрат на управление.
, но и минимальность затрат на управление.
Отклонение реальных выходных параметров 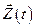 от желаемых
от желаемых 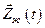 называют ошибкой управления
называют ошибкой управления 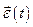 .
.
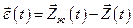 .
.
Для качественной работы проектируемой системы необходимо выполнение следующих условий:
1) минимальность ошибка управления 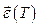 в конечный момент времени
в конечный момент времени 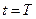 ;
;
2) небольшие ошибки управления 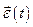 в процессе управления,
в процессе управления, 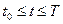 ;
;
3) минимальные затраты энергии на управление (минимальная стоимость управления).
Наиболее часто для описания качества работы системы используется обобщённый критерий, учитывающий эти требования:
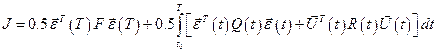 , (8.3)
, (8.3)
где 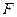 ,
, 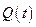 - постоянная и нестационарная положительно полуопределённые
- постоянная и нестационарная положительно полуопределённые 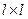 -матрицы соответственно;
-матрицы соответственно;
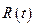 - нестационарная положительно определённая
- нестационарная положительно определённая 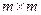 -матрица.
-матрица.
Напомним, чтоматрица называется положительно полуопределённой, если она симметрична 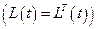 и при любом не нулевом векторе
и при любом не нулевом векторе 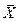
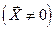 выполняется неравенство:
выполняется неравенство: 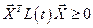 . Если при тех же условиях выполняется строгое неравенство
. Если при тех же условиях выполняется строгое неравенство 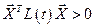 , то матрица
, то матрица 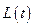 называется положительно определённой.
называется положительно определённой.
Рекомендуется выбирать матрицы 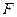 ,
, 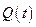 и
и 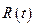 диагональными, с элементами, пропорциональными максимальным допустимым значениям величин
диагональными, с элементами, пропорциональными максимальным допустимым значениям величин 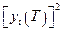 ,
,  и
и 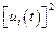 соответственно. Поэтому АКР в этом случае называют синтезом оптимальных систем управления по квадратичному критерию качества.
соответственно. Поэтому АКР в этом случае называют синтезом оптимальных систем управления по квадратичному критерию качества.
Таким образом, задача АКР заключается в поиске такого управления 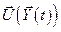 и соответствующей ему траектории
и соответствующей ему траектории 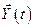 , при которых критерий качества
, при которых критерий качества  (8.3) достигает наименьшего значения.
(8.3) достигает наименьшего значения.
Такая задача АКР называется задачей слежения, т.к. в ней требуется, чтобы реальный выход 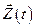 наилучшим образом, с позиции критерия качества
наилучшим образом, с позиции критерия качества  (второе слагаемое в (8.3)), следил за изменением желаемого выходного сигнала
(второе слагаемое в (8.3)), следил за изменением желаемого выходного сигнала 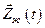 .
.
Преимущество задачи слежения - высокая точность слежения сочетается с малыми затратами на слежения (третье слагаемое в (8.3)).
Пример 2. Если в задаче слежения 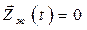 , то такую задачу называют задачей о регуляторе выхода, а критерий качества (8.3) приобретает форму
, то такую задачу называют задачей о регуляторе выхода, а критерий качества (8.3) приобретает форму
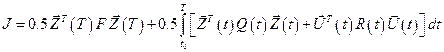 . (8.4)
. (8.4)
Целью задачи о регуляторе выхода является удержание выходных координат объекта 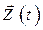 вблизи нуля. Если начальное отклонение выходных координат
вблизи нуля. Если начальное отклонение выходных координат 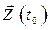 от нуля велико, то управляющее устройство должно приблизить их к нулю и в последующем удерживать около нуля, не расходуя много энергии на управление.
от нуля велико, то управляющее устройство должно приблизить их к нулю и в последующем удерживать около нуля, не расходуя много энергии на управление.
Пример 3. В ряде случаев важно около нуля удерживать не сигнал на выходе ОУ, а все компоненты вектора состояния 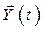 . Если
. Если 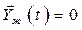 , то задачу называют задачей о регуляторе состояния
, то задачу называют задачей о регуляторе состояния 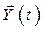 .
.
Критерий качества для задачи о регуляторе состояния имеет вид
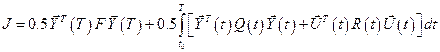 . (8.5)
. (8.5)
Описание такой задачи аналогично описанию задачи о регуляторе выхода, заменив 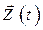 на
на 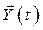 .
.
Пример 4. Для стационарного линейного объекта, который описывается уравнением состояния
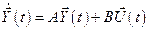 , (8.6)
, (8.6)
критерий качества записывается в виде:
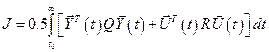 , (8.7)
, (8.7)
где 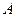 ,
, 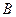 ,
, 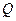 и
и 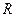 - независимые от времени матрицы.
- независимые от времени матрицы.
При этом на управление  ограничений не наложено, а задаётся ограничение на конечное состояние объекта в форме
ограничений не наложено, а задаётся ограничение на конечное состояние объекта в форме 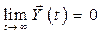 (условие устойчивости), которое эквивалентна асимптотической устойчивости проектируемой системы.
(условие устойчивости), которое эквивалентна асимптотической устойчивости проектируемой системы.
Тогда задача сводится к поиску такого управления 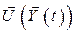 , под действием которого критерий (8.7) достигнет наименьшего значения при выполнении условия асимптотической устойчивости.
, под действием которого критерий (8.7) достигнет наименьшего значения при выполнении условия асимптотической устойчивости.
Рассмотренные примеры задач АКР можно распространить и на нелинейные объекты.
8.2 Синтез регуляторов при жёстко заданной структуре
Как отмечалось выше (п.8.1), при синтезе автоматических систем проектировщиком выбираются структура и параметры управляющих устройств. Остановимся на наиболее простом случае синтеза, если структура уже выбрана, а необходимо только подобрать её параметры.
Рассмотрим одномерный стационарный линейный объект, который описывается уравнениями состояния:
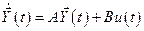 ;
; 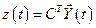 (8.8)
(8.8)
и включен в систему управления так, как показано на рис. 8.1.
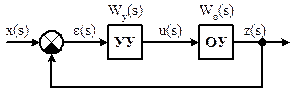 |
Рисунок 8.1 – Схема автоматического управления одномерным стационарным линейным объектом
Пусть передаточная функция управляющего устройства (УУ) 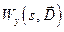 задана, где
задана, где 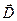 – вектор варьируемых параметров. Для стационарного одномерного объекта квадратичный критерий качества (8.7) можно записать в виде:
– вектор варьируемых параметров. Для стационарного одномерного объекта квадратичный критерий качества (8.7) можно записать в виде:
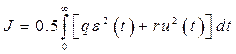 . (8.9)
. (8.9)
Необходимо подобрать так варьируемые параметры 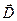 , чтобы выполнялось условие
, чтобы выполнялось условие
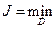 . (8.10)
. (8.10)
Определим составляющие  и
и 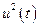 критерия качества (8.9).
критерия качества (8.9).
Из рис. 8.1 видно, что сигнал рассогласования (ошибка регулирования)
 ;
;
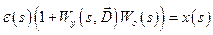 ;
;
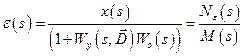 . (8.11)
. (8.11)
Аналогично находим 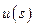 :
:
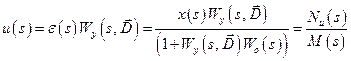 . (8.12)
. (8.12)
Передаточную функцию ОУ 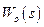 можно определить из уравнений состояния (8.8), записав их в операторной форме:
можно определить из уравнений состояния (8.8), записав их в операторной форме:
 ;
; 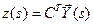 .
.
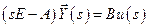 ,
,
где 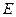 - единичная матрица размерности
- единичная матрица размерности 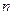 ;
;
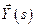 ,
, 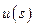 и
и 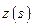 - соответствующие изображения.
- соответствующие изображения.
Тогда передаточная функция ОУ примет вид:
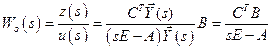 .
.
С учётом того, что в критерии качества (8.9) используются функции времени 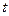 , то для перехода с операторной формы воспользуемся обратным преобразованием Лапласа:
, то для перехода с операторной формы воспользуемся обратным преобразованием Лапласа:
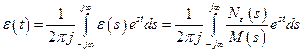 ;
; 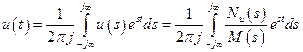 .
.
Тогда
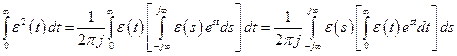 .
.
Из прямого преобразования Лапласа
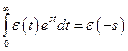
следует, что
 . (8.13)
. (8.13)
Выражение (8.13) называется формулой Парсеваля.
По аналогии
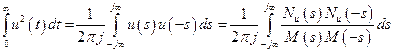 . (8.14)
. (8.14)
Интегралы (8.13), (8.14) вычисляются с помощью методов теории функций комплексного переменного и выражаются через коэффициенты полиномов 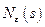 ,
, 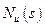 ,
, 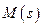 следующим образом. Представим полином
следующим образом. Представим полином 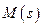 в виде
в виде
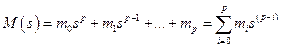 ,
,
а произведение 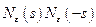 в виде
в виде
 .
.
Тогда интеграл (8.13) можно вычислить из формулы
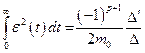 , (8.15)
, (8.15)
где 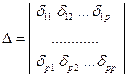 ;
; 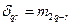 ,
, 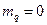 - определитель и его элементы.
- определитель и его элементы.
Определитель 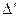 получается из определителя
получается из определителя 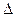 заменой элементов первого столбца величинами
заменой элементов первого столбца величинами 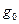 ,
, 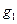 ,...,
,..., 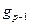 .
.
Аналогично берётся интеграл (8.14).
Определив интегралы (8.14) и (8.15), можно найти критерий качества (8.9) как функцию от варьируемых параметров 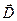 . Из условия минимальности (8.10) критерия
. Из условия минимальности (8.10) критерия  при отсутствии ограничений на
при отсутствии ограничений на 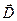 находятся оптимальные параметры
находятся оптимальные параметры 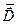 из уравнения
из уравнения
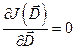 .
.
 2014-02-04
2014-02-04 621
621








