Как и в случае динамического программирования, для простоты рассмотрим задачу о максимальном быстродействии для линейного объекта, описываемого уравнением состояния
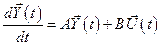 ;
; 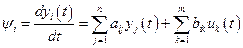 . (7.27)
. (7.27)
В силу стационарности (линейности) уравнения (7.27) переменную 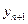 со свойствами (6.3) можно не вводить. Нет также причин для введения переменной
со свойствами (6.3) можно не вводить. Нет также причин для введения переменной 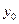 со свойствами (6.4), так как в задаче о максимальном быстродействии
со свойствами (6.4), так как в задаче о максимальном быстродействии 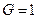 и не зависит от управления
и не зависит от управления 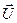 .
.
Запишем принцип максимума (6.22) через функцию Гамильтона (6.21) с учётом (7.27):
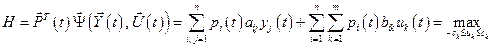 . (7.28)
. (7.28)
Так как от управлений 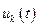 зависит только вторая группа слагаемых в составе (7.28), то принцип максимума приобретёт следующую форму:
зависит только вторая группа слагаемых в составе (7.28), то принцип максимума приобретёт следующую форму:
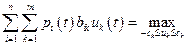 . (7.29)
. (7.29)
Это условие (7.29) должно выполняться для каждого управления 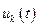
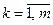 , вследствие чего можно записать:
, вследствие чего можно записать:
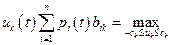 ,
, 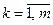 . (7.30)
. (7.30)
Условие (7.30) при существовании на управление ограничений 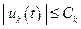 выполняется, если
выполняется, если 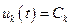 при
при 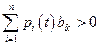 или
или 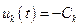 при
при 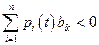 .
.
Отсюда следует, что
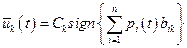 ,
, 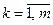 , (7.31)
, (7.31)
Таким образом, в задаче о максимальном быстродействии в случае применения принципа максимума, как и при динамическом программировании, оптимальное управление 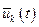 принимает два значения
принимает два значения 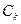 или
или 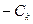 в зависимости от функции
в зависимости от функции 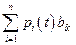 (
( - при динамическом программировании).
- при динамическом программировании).
Как видно из (7.31) для отыскания конкретного управления необходимо знать компоненты 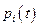 ,
, 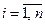 , вектора
, вектора 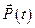 . С этой целью составляется система сопряжённых уравнений (6.26) с учётом линейности уравнения (7.27):
. С этой целью составляется система сопряжённых уравнений (6.26) с учётом линейности уравнения (7.27):
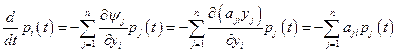 ,
, 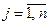 . (7.32)
. (7.32)
Здесь учтено, что 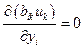 .
.
Таким образом, функцию 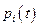 можно найти из системы однородных линейных уравнений, не зависящих от управления
можно найти из системы однородных линейных уравнений, не зависящих от управления  и состояния
и состояния 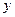 объекта управления.
объекта управления.
Однако так как не задаётся ни начальное 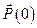 , ни конечное
, ни конечное 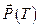 значения вектора
значения вектора 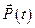 , то такую систему решить нельзя. В этом случае начальное значение вектора
, то такую систему решить нельзя. В этом случае начальное значение вектора 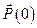 выбирается произвольно. Из (7.32) находятся компоненты вектор
выбирается произвольно. Из (7.32) находятся компоненты вектор 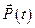 и подставляются в выражение для оптимального управления
и подставляются в выражение для оптимального управления 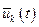 (7.31). После вычисления управления
(7.31). После вычисления управления 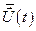 его подставляют в уравнение состояния линейного объекта (7.27), откуда находят вектор состояния
его подставляют в уравнение состояния линейного объекта (7.27), откуда находят вектор состояния 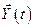 , обусловленный оптимальным управлением
, обусловленный оптимальным управлением 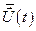 и начальным состоянием
и начальным состоянием 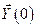 .
.
Если можно подобрать такое  , при котором
, при котором 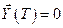 , то начальное значение
, то начальное значение 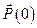 оказалось верным, а найденное управление
оказалось верным, а найденное управление 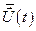 явилось оптимальным. Если
явилось оптимальным. Если 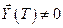 , то выбирается другое начальное значение вектора
, то выбирается другое начальное значение вектора 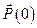 . Последовательный поиск оптимального управления осуществляется с помощью ЭВМ.
. Последовательный поиск оптимального управления осуществляется с помощью ЭВМ.
В некоторых случаях найти оптимальное управление можно, не решая систему сопряжённых уравнений (7.32). Для этого воспользуемся уравнением состояния (7.27) при отсутствии управления 
 ,
, 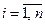 . (7.33)
. (7.33)
В векторной форме уравнения (7.32) и (7.33) примут вид
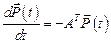 ;
; 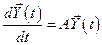 .
.
В общем виде решение уравнения (7.32) можно представить, используя формулу Эйлера:
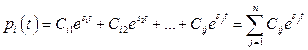 ,
, 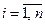 , (7.34)
, (7.34)
где 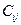 - постоянные интегрирования;
- постоянные интегрирования;
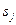 - положительные корни характеристического уравнения, определяемые из сопряжённой системы
- положительные корни характеристического уравнения, определяемые из сопряжённой системы
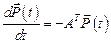 , (7.35)
, (7.35)
где 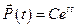 .
.
После подстановки 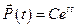 в (7.35) имеем
в (7.35) имеем 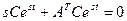 . После сокращения на множитель
. После сокращения на множитель 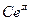 получаем характеристическое уравнение
получаем характеристическое уравнение
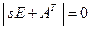 , (7.36)
, (7.36)
где 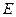 – единичная матрица;
– единичная матрица;
 - комплексная переменная.
- комплексная переменная.
Определив корни характеристического уравнения 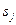 и постоянные интегрирования
и постоянные интегрирования 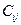 , можно получить выражение оптимального управления
, можно получить выражение оптимального управления 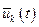 :
:
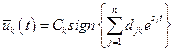 ,
, 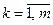 , (7.37)
, (7.37)
где 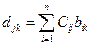 - некоторая константа.
- некоторая константа.
Схематически изменение оптимального управления 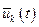 можно представить в виде графика (рис. 7.4), как и в случае динамического программирования, только здесь моменты времени переключения оптимального управления соответствуют корням характеристического уравнения
можно представить в виде графика (рис. 7.4), как и в случае динамического программирования, только здесь моменты времени переключения оптимального управления соответствуют корням характеристического уравнения 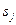 .
.
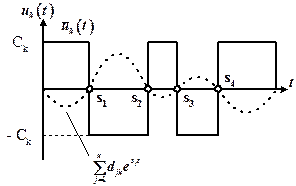 |
Рисунок 7.4 – График переключения оптимального управления 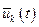
Из рис. 7.4 видно, что оптимальное управление 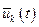 является кусочно-постоянной функцией, имеющей на интервале управления не более
является кусочно-постоянной функцией, имеющей на интервале управления не более 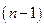 точек разрыва, в которых оно переходит с одной границы области допустимых управлений на другую. Другими словами, оптимальное управление
точек разрыва, в которых оно переходит с одной границы области допустимых управлений на другую. Другими словами, оптимальное управление 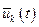 имеет не более
имеет не более 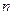 интервалов постоянства, а число переключений управления
интервалов постоянства, а число переключений управления 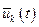 не превышает
не превышает 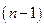 . Это свойство называется теоремой об
. Это свойство называется теоремой об 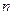 -интервалах (доказана Фельдбаумом).
-интервалах (доказана Фельдбаумом).
Теорема об n-интервалах: если количество действительных корней характеристического уравнения объекта равно 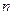 , то число переключений каждого из управлений
, то число переключений каждого из управлений 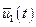 ,
, 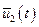 , …,
, …, 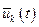 не превышает
не превышает 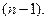
 2014-02-04
2014-02-04 848
848








