Главное открытие немецкого ученого В. Лаунхардта (W. Launhardt), основная работа которого была опубликована в 1882 г., — метод нахождения пункта оптимального размещения отдельного промышленного предприятия относительно источников сырья и рынков сбыта продукции.
Решающим фактором размещения производства у В. Лаунхардта, так же как и у Й.Тюнена, являются транспортные издержки. Производственные затраты принимаются равными для всех точек исследуемой территории. Точка оптимального размещения предприятия находится в зависимости от весовых соотношений перевозимых грузов и расстояний. Для решения этой задачи В. Лаунхардт разработал метод весового (или локационного) треугольника.
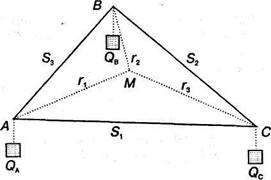
Рис. 3.2 Локационный треугольник В. Лаунхардта
Пусть требуется найти пункт размещения нового металлургического завода. Известны пункт добычи железной руды — точка А (рис. 3.2), пункт добычи угля — точка В и пункт потребления металла — точка С. Транспортный тариф равен t (на 1 т.км). Расход руды на выплавку 1т металла равен а, расход угля — b.. Известны также расстояния между пунктами (стороны локационного треугольника): АС = S1; BC=S2; AB=S3
Возможным пунктом размещения металлургического завода может быть в принципе каждая из трех точек размещения источников руды и угля и потребителя металла. В этих случаях суммарные затраты, связанные с перевозкой всех необходимых грузов для потребления 1 т металла, будут равны: (bS3 + S 1 )t — при размещении завода в точке А; (aS3 + S 2 )t — при размещении завода в точке В; (aS1 + bS 2 )t — при размещении завода в точке С. Наилучшим пунктом размещения завода из рассмотренных трех будет тот, в котором транспортные затраты минимальны. Однако искомый пункт размещения может не совпадать ни с одной из вершин локационного треугольника, а находиться внутри него в некоторой точке М.
Расстояния от внутренней точки М до вершин треугольника составляют:
AM = r 1, ВМ = r 2, СМ = r 3. Тогда транспортные издержки при размещении металлургического завода в точке М будут равны Т= (ar 1 +br 2 +r 3 )t. Выполнение требования Т → min дает точку оптимального местоположения предприятия.
Данная задача имеет геометрическое и механическое решения.
Геометрический метод нахождения точки размещения состоит в том, что на каждой из сторон локационного треугольника строится треугольник, подобный весовому (стороны которого относятся как а:Ь: 1 ). Затем вокруг построенных таким образом треугольников описываются окружности, точка пересечения которых и является точкой минимума транспортных издержек. Этот метод — для случая, когда соотношения расстояний S1, S2, S3 соответствуют свойству треугольника (одна сторона меньше суммы двух других). В противном случае (например, когда S1 > S2+S3) точка минимума транспортных затрат будет совпадать с одной из вершин локационного треугольника.
Механическое решение рассматриваемой задачи основывается на аналогии с методом нахождения точки равновесия сил. При этом веса руды, угля, металла выступают в качестве сил, с которыми притягивают производство соответствующие вершины локационного треугольника. Искомая точка является точкой равновесия трех связанных нитей, проходящих через вершины локационного треугольника. При этом к концам нитей подвешены грузы (Qa, Qb, Qc), пропорциональные a, b, 1. Весовой треугольник В. Лаунхардта — одна из первых в экономической науке физических моделей, используемых для решения теоретических и практических задач.
Изложенный метод нахождения оптимального размещения предприятия применим и для большего числа точек (видов сырья) при условии, что они образуют выпуклый многоугольник.
 2014-02-04
2014-02-04 2313
2313








