Парная линейная регрессия. При регрессионном анализе изучается связь между зависимой пе­ременной и одной или несколькими независимыми перемен­ными

При регрессионном анализе изучается связь между зависимой пе­ременной 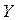и одной или несколькими независимыми перемен­ными .

Проведём анализ парной регрессии, когда независимая переменная одна. Предположим, что переменная 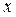(как прави­ло, неслучайная величина) принимает некоторые фиксирован­ные значения 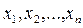. Соответствующие значения зависимой переменной 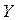имеют разброс вследствие погрешности из­мерений и различных неучтенных факторов: 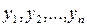. Пред­положим, что связь между переменными линейная (рис. 4.34), тогда соответствующая регрессионная модель имеет вид:

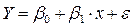, (4.1)

где 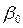и - параметры линейной регрессии;

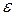- случайная ошибка наблюдений.

Предполагается, что математическое ожидание 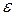равно нулю, а дисперсия постоянна: , .

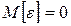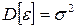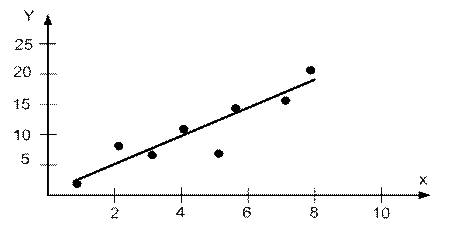
Рисунок 4.34. Парная линейная регрессия

Задача регрессионного анализа сводится к оценке парамет­ров регресси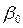и и , проверке гипотезы о значимости модели и оценке её адекватности: достаточно ли хорошо согласуется мо­дель (4.1) с результатами наблюдений?

Для оценки параметров регрессии используется метод наи­меньших квадратов: в качестве оценок принимаются такие зна­чения 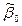и 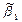, которые минимизируют сумму квадратов откло­нений 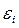наблюдаемых значений 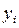от расчетных:

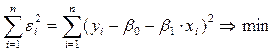. (4.2)

Приравнивая к нулю производные по 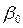и , получаем зависимости для оценивания параметров модели (4.1):

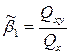(4.3)

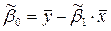, (4.4)

где

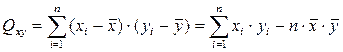; (4.5)

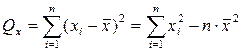(4.6)

Прогнозируемое по модели (4.1) значение зависимой переменной:

.

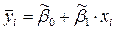Разности между наблюдаемыми и прогнозируемыми значениями называются остатками, а соответствующая сумма квадратов - остаточной суммой квадратов:

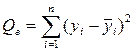. (4.7)

Пусть

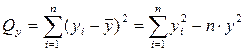- (4.8)

общая сумма квадратов;

сумма квадратов, обусловленная регрессией:

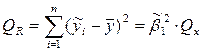. (4.9)

Тогда остаточную сумму квадратов можно вычислить, ис­пользуя основное тождество дисперсионного анализа:

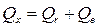. (4.10)

Парная линейная регрессионная модель называется незначимой, если параметр 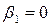. Для проверки нулевой гипотезы 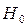: 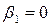используется статистика

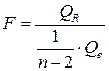. (4.11)

При заданном уровне значимости 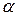она сравнивается с квантилью распределения Фишера с числами степеней свободы 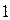и 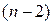. Если оказывается 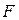>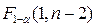, то нулевая гипотеза отклоняется: регрессионная модель статисти­чески значима.