Уравнение с угловым коэффициентом.
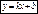 k= tg α – угловой коэффициент.
k= tg α – угловой коэффициент.
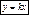
Если b=0 то прямая проходит через начало координат. Уравнение примет вид
Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.
Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет вид 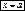 и пройдет параллельно оси оу.
и пройдет параллельно оси оу.
Общее уравнение прямой.

A, B, C – произвольные числа, причем А и В не равны нулю одновременно.
· Если В=0, то уравнение имеет вид 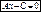 или
или 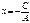 . Это уравнение прямой, параллельной оси оу. и проходящей через точку
. Это уравнение прямой, параллельной оси оу. и проходящей через точку 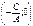
· Если В≠0, то получаем уравнение с угловым коэффициентом 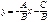 .
.
· Если А=0, то уравнение имеет вид 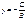 . Это уравнение прямой, параллельной оси ох.
. Это уравнение прямой, параллельной оси ох.
· Если С=0, то уравнение проходит через т. О (0;0).
Уравнение прямой, проходящей через точку, в данном направлении.
т М (х0;у0).
Уравнение прямой записывается в виде 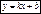 .
.
Подставим в это уравнение точку М 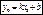
Решим систему:
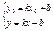
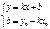
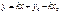
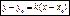
Уравнение прямой, проходящей через 2 точки.
К (х1;у1) М (х2;у2)
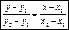
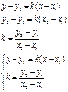
Уравнение прямой в отрезках.
К (а;0); М (0;b)
Подставим точки в уравнение прямой:
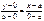
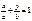
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.
М0 (х0;у0). 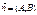
Возьмем произвольную точку М (х;у). 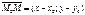
Т.к. 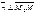 , то
, то 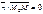
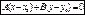
Нормальное уравнение прямой.
Уравнение прямой можно записать в виде:
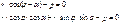
Т.к. 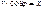 ;
;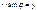 , то:
, то: 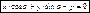
 2014-02-04
2014-02-04 335
335








