Частица в потенциальной яме. Дискретность энергетического состояния

Рассмотрим частицу, которая находится в потенциальном поле имеющем форму ямы.

Как было показано в § 5 волновые функции частицы области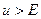

Если 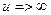то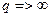

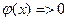
Таким образом случай бесконечно глубокой ямы при x<0, x>a,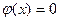

Если 0<x<a то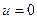

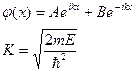
Из левого граничного условия следует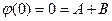

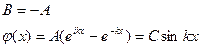
Из второго граничного условия следует

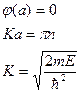
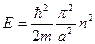
Таким образом частица находится в потенциальной яме, то её энергетический спектр дискретен.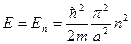

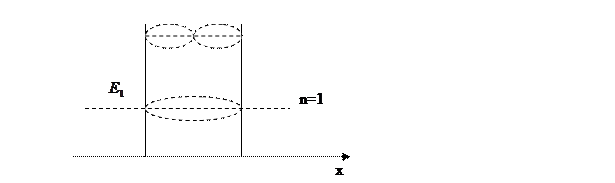
Таким образом, частица которая находилась в потенциальной яме может принимать лишь дискретное значение энергии под действием постоянной скорость E не непрерывна.

Условие дискретности энергии спектр направление связано с характеристикой движения частиц. Если движение ограниченно, то спектр энергии дискретный.

Если движение частицы не ограниченно, то её энергетический спектр непрерывен.

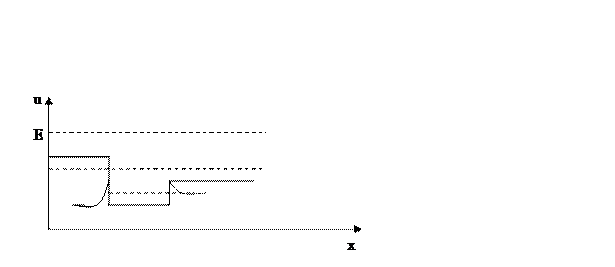
E>u движение не ограниченно