Принцип неопределенности Гейзенберга. Рассмотрим одномерный случай, когда

Рассмотрим одномерный случай, когда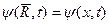

Если волновая функция частицы представляют собой волновой пакет протяжённостью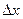

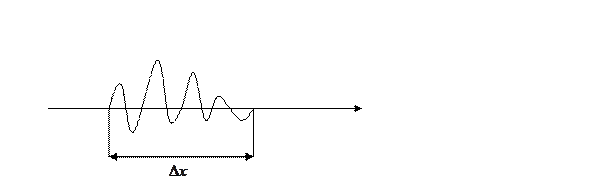
Таким образом очевидно вероятность обнаружения частиц будет отличаться от 0 только там где существует волновой пакет.

Таким образом о местоположение частицы можно говорить лишь с некоторой не определённостью 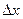Для определения которой выполним § 2.9

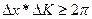
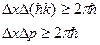
Где 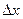не определённость координатами частицы, а 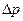не определённость её импульсом.

Соотношение неопределенности Гейзенберга для координат и импульса.

Если мы точно знаем координаты частицы 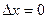, то мы не знаем, как она двигается .

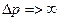Если мы находимся в некоторой точке, и мимо нас пролетает частица, то есть мимо нас распространяется волновой пакет, то мы будем наблюдать импульс колебаний.

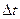длительность импульса определяет неопределенность времени, когда частица находится в данной точке пространства, то есть частица находилась в данной точке пространства в течение 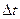с разной вероятностью. В §1.7 было показано

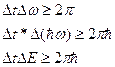
То есть если мы точно знаем время, то не знаем энергию.