2014-02-02
2362
Закон количества движения имеет большое значение в газовой динамике, особенно для решения прикладных задач. Уравнение количества движения применительно к жидкости было получено Эйлером.
Как известно, закон количества движения в механике устанавливает, что импульс силы равен изменению количества движения тела за время действия силы и записывается уравнением
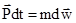, (1)
или
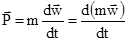(2)
Произведение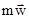 
- называется количеством движения, если обозначить 
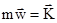, то
. (3)
Уравнение Эйлера представляет собой распространение формулы (10) на случай движения жидкости или газа: производная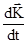 
должна равняться равнодействующей всех внешних сил, действующих на жидкость, которая находится в объеме внутри контура, т.е.
. (4)
Если силами трения и тяжести можно пренебречь, то
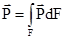и
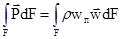. (5)
Применим полученное уравнение к цилиндрической камере сгорания (к цилиндру, ограниченному сечениями 1-1 и 2-2). Контуром (контрольной поверхностью) в этом случае являются боковая и торцевые поверхности. На боковой поверхности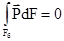 
, т.к. на цилиндрической поверхности силы давления взаимно уравновешиваются.
|
|
|
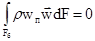, т.к. поверхность непроницаема и wп = 0. Оставшиеся участки контрольной поверхности (контура) F1 и F2 представляют собой поперечные сечения, в пределах которых давления, плотности и скорости можно считать постоянными. Тогда
,
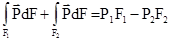
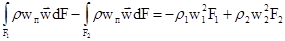т.к. количество движения втекающей жидкости считается отрицательным, а вытекающей – положительным.
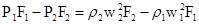(6)
Выражение (6) аналогично выражению (6)
Принимая во внимание уравнение расхода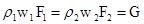 
, формулу (13) можно представить в таком виде:
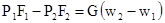или
. (7)
Формула (7) называется уравнением количества движения в полных импульсах, а величина Ф = РF + Gw – полным импульсом.
