Правила суммы и произведения. 1.Правило суммы: если объект А может быть выбран n способами, а объект В – m способами, то выбор «А или В» может быть осуществлен n+m способами

1. Правило суммы: если объект А может быть выбран n способами, а объект В – m способами, то выбор «А или В» может быть осуществлен n+m способами.

Пример. Если на одной полке книжного шкафа стоит 30 различных книг, а на другой - 40 различных книг (и не таких, как на первой полке), то выбрать одну книгу из стоящих на этих полках можно 30 + 40 = 70 способами.

При использовании правила сложения нужно следить, чтобы ни один из способов выбора объекта А не совпадал с каким-нибудь способом выбора объекта В, т. е. чтобы ни одна комбинация не попала сразу в два класса. Если такие совпадения имеются, правило сложения в ранее сформулированной форме утрачивает силу, и мы получаем m + n – k способов выбора, где k — число совпадений.

2. Общее правило суммы: Если объект А можно выбрать m способами, а объект В — n способами, причем при k способах одновременно выбираются и А и В, то выбор «А или В» можно осуществить m + n – k способами.

Пример. Сколько чисел в первой сотне, не делящихся ни на 2, ни на 3?

Решение: Легче вычислить сначала количество чисел первой сотни, делящихся на 2 или на 3. Каждое второе число в натуральном ряде делится на 2, каждое третье— на 3. Поэтому в первой сотне есть 50 чисел, делящихся на 2, и 33 числа (неполное частное от деления 100 на 3), делящихся на 3. Но среди первых и вторых имеются числа, делящиеся и на 2, и на 3, т. е. делящиеся на 6. На 6 делится каждое шестое число в натуральном ряде. Если 100 разделить на 6, то неполное частное будет равняться 16, т. е. 16 чисел в первой сотне делится на 6. Итак, количество чисел в первой сотне, делящихся на 2 или на 3, равно 50 + 33 – 16 = 67. Все остальные не делятся ни на 2, ни на 3. Этих чисел 100 – 67 = 33.

3. Правило произведения: если объект А может быть выбран n способами и после каждого из таких выборов объект В – m способами, то выбор «А и В» в указанном порядке может быть осуществлен n*m способами.

Пример. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье - чай и компот. Сколько различных обедов можно составить из указанных блюд?

Решение: Первое блюдо можно выбрать одно из трех (борщ, солянку или грибной суп), второе блюдо тоже одно из трех (мясо с макаронами, рыбу с картошкой или курицу с рисом), на десерт только два варианта (чай или компот). Используя правило произведения, получаем: 3х3х2=18.

Пример. В классе 25 человек. Сколькими способами:

а) можно распределить между ними два различных учебника;

б) можно распределить между ними два различных учебника так, чтобы никто не получил оба учебника;

Решение: а) Первый учебник может получить любой из 25 учащихся.Кто бы ни получил первый учебник, второй может достаться снова любому из 25, ведь в условии не сказано, что каждый должен получить не более одного учебника. Всего имеем 25* 25 = 625 способов.

б) В отличие от предыдущего задания, никто не должен получить оба учебника. Поэтому для каждого из 25 вариантов выбора обладателя первого учебника есть 24 способа выбора обладателя второго учебника. Всего имеем 25*24 = 600 способов.

Рассмотрим примеры, использующие правила суммы и произведения.

Пример. Сколькими способами из 28 костей домино можно выбрать две кости так, чтобы их можно было приложить друг к другу (т.е. чтобы какое-то число очков встретилось на обеих костях)?

Решение. Сначала выберем одну кость. Это можно сделать 28 способами. При этом в случаях выбранная кость окажется "дублем", т.е. костью вида 00, 11, 22, 33, 44, 55, 66, а в 21 случае - костью с различными числами очков (например, 05, 13 и т.д.).В первом случае вторую кость можно выбрать 6 способами (например, если на первом шагу выбрана кость 11, то на втором шагу можно взять одну из костей 01, 12, 13, 14, 15, 16).Во втором же случае вторую кость можно выбирать 12 способами (для кости 35 подойдут кости 03, 13, 23, 33, 34, 36, 05, 15, 25, 45, 55, 56). По правилу произведения в первом случае получаем 7*6=42 выбора, а во втором 21 * 12 = 252 выбора. Значит по правилу суммы получаем 42 + 252 = 294 способов выбора пары.

Пример. Сколько существует четырехзначных чисел, у которых все цифры нечетные? Сколько существует четырехзначных чисел, в записи которых есть хотя бы одна четная цифра?

Решение. Всего нечетных цифр - пять, поэтому выбор k-й цифры числа может быть сделан n_к=5 способами (к=1, 2, 3, 4), а количество четырехзначных чисел, у которых все цифры нечетные, равно 5*5*5*5=625. Чтобы ответить на второй вопрос, проще не определять последовательно, сколько существует чисел, в записи которых ровно одна четная цифра, две цифры, три цифры, четыре цифры, а воспользоваться полученным ответом на первый вопрос. Все четырехзначные числа, а их 9999-999=9000, делятся на две группы: те, в записи которых все цифры нечетные, и те, в записи которых есть хотя бы одна четная цифра. Следовательно, количество чисел второго типа равно 9000-625=8375.

Пример. Из города А в город В ведут пять дорог, а из города В в город С — три дороги. Пусть, кроме того, из города А в город D можно попасть двумя путями, из D в C — четырьмя (рис.1). Сколькими способами можно добраться из А в С?

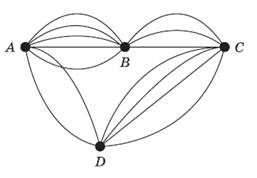
Рис. 1. Варианты перемещения между городами

Решение: Возможны два случая: путь из А в С проходит через город В или через город D. В каждом из этих случаев число возможных маршрутов легко подсчитать, воспользовавшись правилом произведения. В первом случае имеется 5*3 = 15 маршрутов; во втором — 2*4 = 8. Складывая, получаем общее число маршрутов: 15 + 8 = 23.

Правило суммы и произведения – это общие правила решения комбинаторных задач. Кроме них в комбинаторике пользуются формулами для подсчета числа отдельных видов соединений, которые встречаются наиболее часто.