Примеры решения задач. 3адача 1 Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет

3адача 1 Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет.

Решение: Порядок расположения элементов имеет значение и в диаграмме 4 столбца, а ручка тоже четырехцветная, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска столбцов не повторяется (в условии сказано, что столбцы имеют разные цвета), то это перестановка без повторения. Итак, P_n = n! = 4! = 1×2×3×4 = 24

Ответ: столбцы можно закрасить 24 способами.

3адача 2. Имеется 5 кружков: 3 белых и 2 черных. Сколько различных узоров можно получить, располагая кружки в ряд.

Решение: Порядок расположения элементов имеет значение и в узоре 5 кружков, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска кружков повторяется (в условии сказано, что 3 белых и 2 черных), то это перестановка с повторением. Итак,

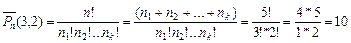
Ответ: узор можно составить 10 способами.

3адача 3 Сколько словарей надо издать, чтобы можно было непосредственно выполнить перевод с любого из 5 языков на любой из 5 языков.

Решение: Порядок имеет значение (так как русско-английский и англо-русский словари различны) и не все элементы присутствуют в соединении (а только 2 из 5), значит, это размещение. Так как языки различны, то это размещение без повторения. Итак,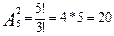

Ответ: надо составить 20 словарей.

3адача 4 Семиклассники написали контрольную работу. Возможные оценки 2, 3, 4, 5. Сколько вариантов расстановки оценок в журнале, если в списке 10 учеников.

Решение: Порядок имеет значение и не все элементы присутствуют в соединении, значит, это размещение. Так как оценки могут повторяться, то это размещение с повторением. Итак,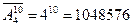

Ответ: может быть 1048576 различных комбинаций оценок.

3адача 5. 12 человек играли в городки. Сколькими способами они могут разбиться на команды по 4 человека в каждой.

Решение: Порядок расположения игроков в команде не имеет значения, следовательно, это сочетание. А так как игроки не повторяются (все члены команды различные люди), то это сочетание без повторения. Итак,

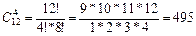
Ответ: игроки могут разбиться на команды по 4 человека в каждой 495 способами.

3адача 6. На уроке технологии учитель предложил школьникам выбрать для поделки 10 листов цветной бумаги из предложенных 6 цветов. Сколько вариантов выбора есть у учеников (наборы, отличающиеся лишь расположением листов цветной бумаги на парте считать одинаковыми)?

Решение: Порядок расположения листов цветной бумаги на парте не имеет значения, следовательно, это сочетание. А так как цвета повторяются, то это сочетание с повторением. Итак, 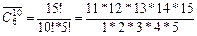=3003

Ответ: выбрать цветную бумагу для поделки можно 3003 способами.

3адача 7 В группе 25 студентов, из которых 5 отличников, 11 хорошистов и остальные троечники. Сколькими способами можно выбрать группу для выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника.

Решение: Сначала узнаем сколькими способами можно выбрать 3 хорошистов из 11 человек. Порядок расположения студентов не важен, значит, это сочетание. А так как люди в группе не повторяются, то это соединение – сочетание без повторения. Итак, одного хорошиста можно выбрать 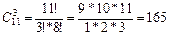способами. Аналогично рассуждая, приходим к тому, что 1 отличника можно выбрать 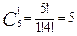способами и одного троечника можно выбрать 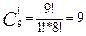способами. Так как команда для выполнения лабораторной работы выбирается одновременно, т.е. 5 хорошистов, затем 1 отличник, затем 1 троечник, то, применив правило произведения, получим: 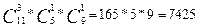способами.

Ответ: группу для выполнения лабораторной работы можно составить 7425 способами.

3адача 8. Девочки на уроке труда приготовили пирожные и пригласили на чай трех мальчиков. Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку.

Решение: Выберем для 3 человек чашки из 4 имеющихся. Порядок расположения элементов имеет значение, и не все элементы входят в соединение, значит, это размещение. Но так чашки не повторяются, то это размещение без повторения. Итак, из 4 чашек 3 можно выбрать способами. Аналогично рассуждая, получим, что из 5 блюдец 3 можно выбрать 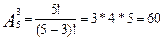способами, а из 6 ложек 3 можно выбрать 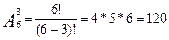способами. 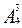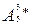Так как блюдце, чашка и ложка входят в набор одновременно, то стол можно накрыть *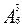=24*60*120=172800 способами.