Соединения без повторений

При определении вида соединения удобно пользоваться следующей схемой (рис.2):

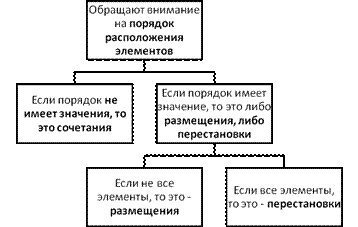
Рис. 2. Схема выбора вида соединения

Пусть дано множество М, состоящее из n элементов.

Определение. Перестановки – всевозможные упорядоченные множества, составленные из всех элементов данного множества. Число всевозможных перестановок из n элементов обозначают Рn и находят по формуле

Р_n= n! (1),

где n!= 1×2×3× … ×n, 0!=1 по определению.

Пример. Сколько перестановок можно составить из трех букв а, в, с?

Решение: Р₃=1×2×3=6. Действительно: авс, вас, асв, сав, вса, сва.

Пример. Сколькими способами можно переставить буквы в слове «треугольник»?

Решение: Т.к. все буквы в данном слове разные, т.е. нет повторений, то можно воспользоваться формулой (1): Р₁₁=11!=39916800.

Определение. Размещениями из n по m называются всевозможные упорядоченные подмножества, содержащие m элементов из данных n. Обозначаются и вычисляются по формуле:

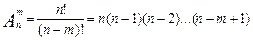(2)

Пример. Сколько можно составить четырехзначных чисел, содержащих различные цифры из 5 цифр.

Решение: Четырехзначное число – это упорядоченная последовательность цифр, т.е. имеем дело с размещениями без повторений:

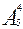=5×4×3×2=120.

Пример. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами может быть составлено расписание на 1 день?

Решение: .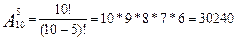

Определение. Сочетаниями из n по m называются всевозможные неупорядоченные подмножества данных n элементов, состоящие из m элементов. Для подсчета их числа используются следующие обозначение и формула:

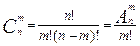(3)

Пример. Сколькими способами можно из 7 различных открыток выбрать три?

Решение: Совокупность трех открыток является неупорядоченным подмножеством семи открыток, поэтому имеем дело с сочетаниями:

.

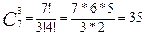Пример. Из группы в 25 человек нужно выбрать троих для работы на субботнике.

Решение: Если выбирать их последовательно, сначала первого, потом второго, потом третьего, то получим 25 * 24 * 23. Но так как нас не интересует порядок выбора, а только количество выбранных человек:

25!/(3!*22!)