2014-02-04
901
Аксиома 4. Коммутативность.
Предпочтение исхода ai исходу aj не зависит от порядка, в котором они названы и представлены.
Если ai предпочтительнее aj и существует исход ak, не оцениваемый относительно этих исходов, тогда вероятностная смесь исходов ai и ak предпочтительнее вероятностной смеси исходов aj и ak. Т.е. отношение предпочтения (безразличия) между двумя исходами не нарушается наличием третьего исхода.
При выполнении всех 5 аксиом существует функция полезности, однозначно определенная на множестве всех альтернатив с точностью до монотонного строго возрастающего линейного преобразования, т.е. полезность измеряется в шкале интервалов. Функция полезности может быть как непрерывной, так и дискретной, в зависимости от типа показателей исходов операции (ПИО). Функция полезности называется прямой, если чем больше ПИО, тем он полезнее, и обратной, если чем выше ПИО, тем он менее полезен.
Все известные способы определения функции полезности носят приближенный характер и строятся на основе: анализа влияния исходов исследуемой операции на операцию более высокого уровня иерархии, экспертных оценок, аппроксимации.
|
|
|
Представление аппроксимации полезности:
1) 
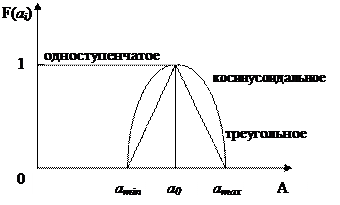Одноступенчатое представление может быть приемлемым для операций, в которых показателем исхода является срок выполнения работ, например, подготовка презентации на выставке. Исходы – фактическое время готовности. Время начала презентации a0 – характерная точка. Полезность системы равна 1, если ai < a0 и полезность равна 0, если ai > a0.
2) и 3) Косинусоидальное и треугольное представление применимо для операций, в которых ПИО – интервал времени. Например, подготовка системы телеконференции в локальной сети. Характерная точка a0 – установленное время готовности.
4.2. Оценка сложных систем в условиях определенности
Производится с помощью методов векторной оптимизации. Пусть K={k1, k2, …kn} –векторный критерий, A={ ai } – множество альтернатив, K(ai) – векторная оценка альтернативы ai. Общая задача векторной оптимизации:
K(a) → opt K(ai) (4.1)
ai ÎA
где opt – оператор оптимизации.
Как правило, не существует альтернативы, оптимальной по всем параметрам.
1 этап. Определяются частные показатели и критерии эффективности.
2 этап. Находится множество Парето, формулируется задача многокритериальной оптимизации.
3 этап. Задача решается путем скаляризации критериев, т.е. устранения неопределенности.
Принцип Парето
Множество Парето – подмножество А* множества альтернатив А, которое задается свойством его элементов:
" a ÎA $ a *ÎA*: K(a *) ≥ K(a). (4.2)
K(a *) ≥ K(a) означает, что
" i ki(a *) ≥ ki(a) и $ i': k i’ (a *) > k i’ (a). (4.3)
|
|
|
Множество Парето (переговорное множество, множество компромиссов) включает альтернативы, более предпочтительные по сравнению с альтернативами из множества A\A*. При этом две любые альтернативы ai и aj из множества Парето по предпочтению несравнимы, т.е. если ai предпочтительнее aj по одним группам критериев, то aj предпочтительнее ai по другим группам критериев.
4.3. Методы решения задач векторной оптимизации
· Метод выделения главного критерия.
ЛПР выделяет один, главный критерий, а остальные выводятся в состав ограничений (т.е. для них указываются границы изменения). Недостаток: нет смысла глубокого исследования системы.
· Метод лексикографической оптимизации
Критерии упорядочиваются по значимости, самый важный №1 и т.д. На первом шаге выбирается подмножество А1ÌА с наилучшими оценками по 1-му критерию. Если оно состоит из 1 элемента, то эта единственная альтернатива признается наилучшей. В противном случае выбирается А2ÌА1 с наилучшими оценками по 2-му критерию и т.д. Недостаток: могут быть использованы не все, а только наиболее важные критерии (с точки зрения ЛПР).
· Метод последовательных уступок
Для каждого из проранжированных о важности критериев назначается допустимое отклонение значения критерия от наилучшего. На первом шаге строится подмножество А1ÌА, для которого отклонение оценки по 1-му критерию от его экстремального значения не превышает допустимого отклонения (уступки). Далее аналогично строятся подмножества А2ÌА1, А3ÌА2 и т.д. При этом уступки назначаются такими, чтобы на каждом шаге в подмножестве А i было более одного элемента.
· Человеко-машинные процедуры
Сочетание возможностей ЭВМ по быстрому проведению расчетов и способностей человека к восприятию альтернатив в целом и сравнения их по отдельным критериям.
4.4. Методы свертывания векторного критерия в скалярный
k(a)= f (k1(a), k2(a)… k n (a)), k(a) → extr (4.4)
a ÎA
Решаются следующие задачи:
1) Обоснование допустимости свертки. Рассматриваемые показатели эффективности должны быть однородными. Показатели эффективности делятся на три группы: показатели результативности, ресурсоемкости, оперативности. Разрешается свертка показателей отдельно в каждой группе.
2) Нормализация критериев для их сопоставления. Проводится подобно нормировке показателей: для каждого критерия определяется оптимальное значение и вместо k i (a) рассматриваются k i (a)/ki opt.
3) Учет приоритетов критериев (весовых коэффициентов). Строится вектор коэффициентов важности критериев l=(l1, l2…l n), Sl i =1. Вместо исходной векторной оценки K(a) = (k1(a), k2(a)… k n (a)) рассматривается новая векторная оценка (l1k1(a), l2k2(a)… l n k n (a)).
4) Построение f –свертки.
а) Аддитивная свертка – сумма взвешенных нормированных частных критериев:
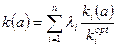. (4.5)
Используется принцип: справедливым следует считать такой компромисс, при котором суммарный уровень абсолютного снижения значений одного или нескольких показателей не превышает суммарного уровня абсолютного увеличения значений других показателей. Недостаток: аддитивные критерии не вытекают и объективной роли частных критериев, это формальный математический прием. Низкие оценки по одним критериям могут компенсироваться высокими оценки по другим критериям.
б) Мультипликативная свертка – произведение
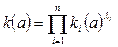. (4.6)
При равно важности критериев l i =1. Используется принцип справедливой относительной компенсации: суммарный уровень относительного снижения значений одних критериев не превышает суммарного уровня относительного увеличения других критериев.
В математической форме такое условие оптимальности имеет вид:
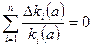. (4.7)
Полагая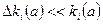 
, получаем
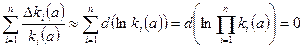. (4.8)
Достоинства: не требуется нормировки частных критериев.
|
|
|
Недостатки: компенсирует недостаточную величину одного частного критерия избыточной величиной другого, сглаживает уровни частных критериев за счет неравнозначных первоначальных значений.
в) Если недопустима компенсация значений одних показателей другими, т.е. требуется обеспечить равномерное подтягивание всех показателей к наилучшему уровню, то используют следующую агрегирующую функцию:
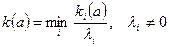. (4.9)
г) Общий случай функции свертки:
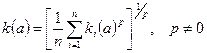, (4.10)
где p – допустимая степень компенсации малых значений одних показателей большими значениями других равноценных показателей: чем больше p, тем больше степень возможной компенсации. При p → – ¥ не допускается компенсация, формула (4.10) дает результаты, совпадающие с формулой (4.9). При p →0 – обеспечение примерно одинаковых уровней частных показателей, в пределе (4.10) будет совпадать с (4.6). При p =1 – совпадение (4.10) и (4.5). Во всех предельных случаях предполагается l i =1/ n.
д) Если одни показатели желательно увеличивать, а другие уменьшать, то иногда используют функцию агрегирования в виде отношения одних показателей к другим, например:
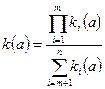. (4.11)
В числителе произведение значений показателей, которые нужно увеличить, в знаменателе сумма значений показателей, которые нужно уменьшать. Часто первая группа связана с целевым эффектом, вторая – с затратами на его достижение. При этом показатели не должны быть однородными.
Условия применимости рассмотренных методов из-за их эвристического характера не могут быть четко сформулированы. От этого недостатка свободна группа методов, основанная на теории полезности.
Лекция 5 Оценка сложных систем в условиях риска
и в условиях неопределенности
5.1. Оценка сложных систем в условиях риска на основе функции полезности
Операции, выполняемые в условиях риска, называются вероятностными. Нет однозначного соответствия между операциями и исходами. Каждой системе ai (i =1,2… n) ставится в соответствие множество исходов { yk }, k =1,2… m с известными условными вероятностями p (yk/ai). Эффективность систем в вероятностных операциях находится как мат.ожидание функции полезности на множестве исходов: K (a)= Ma [ F (y)]. При дискретных значениях показателей исходов yk, k =1,2… m, имеющих условные вероятности p (yk/ai) и полезность F (yk):
|
|
|
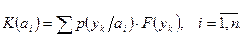
При непрерывных значениях показателей исходов:
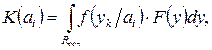
где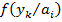 
- плотность вероятностей исходов, 
- допустимая область векторного пространства исходов.
Критерий оптимальности для вероятностных операций имеет вид:
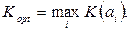
Это оценка «в среднем».
Главный недостаток – не исключен случай выбора неоптимальной системы для конкретной реализации системы (или операции). Однако при многократном повторении операции оптимальная в среднем система приведет к наибольшему успеху.
Т.е. сведение задачи оценки систем к вероятностной постановке применимо для операций, имеющих массовый характер, для которых существует возможность определить объективные показатели исходов, вероятностные характеристики и законы распределения вероятностей на множестве исходов операции.
Кроме оптимизации «в среднем» в вероятностных операциях используются и другие критерии оценки систем:
- максимум вероятности случайного события,
- максимум степени вероятностной гарантии достижения результата не ниже требуемого уровня,
- минимум среднего квадрата отклонения результата от требуемого,
- минимум дисперсии результата.
Пример. Оценка вариантов размещения оборудования по производству некоторого продукта. Исследуемая операция – производство деталей; системы ai – варианты размещения оборудования, ПИО (показатель исхода операции) – число деталей yk за некоторый период времени.
| Исходные данные | вычисляем | |||
| ai | yj | p (yj/ai) | F (yj): | K (ai) |
| Вариант 1 | 0.3 | 0.8 | 0.51 | |
| 0.5 | 0.5 | |||
| 0.2 | 0.1 | |||
| Вариант 2 | 0.25 | 0.8 | 0.515 | |
| 0.6 | 0.5 | |||
| 0.15 | 0.1 | |||
| Kopt=max (K (ai))= K (a2)=0.515 |
5.2. Оценка сложных систем в условиях неопределенности
Многие операции в организационно-технических системах не могут быть сведены к детерминированным или вероятностным. Например:
1) наличие в управляемой системе элементов (подсистем) или ЛПР, осуществляющих управление на основе субъективных моделей, что приводит к большому разнообразию поведения системы,
2) алгоритм управления строит сама система управления,
3) в системе отсутствуют объективные критерии оценивания достижения целевого и текущего состояний объекта и т.п.
Условия оценки эффективности систем для неопределенных операций можно представить в виде таблицы:
| ai | yj | K(ai) | |||
| y1 | y2 | … | ym | ||
| a1 | k11 | k12 | … | k1m | |
| a2 | k21 | k22 | … | k2m | |
| ... | … | … | … | … | |
| an | kn1 | kn2 | … | knm |
{ ai } – вектор управляемых параметров, определяющий свойства системы, i =1,2…n,
{ yj } – вектор неуправляемых параметров, определяющий состояние обстановки, j =1,2…m,
kij – значение эффективности системы ai для состояния обстановки yj,
K(ai) – эффективность системы ai.
При этом нет данных о том, с какой вероятностью может появиться каждое состояние.
В зависимости от характера неопределенности операции могут делиться на игровые и статистически неопределенные. В игровых операциях неопределенность вносит своими сознательными действиями противник, ими занимается теория игр. Условия статистически неопределенных операций зависят от природы (объективной действительности).
Нет единого критерия оценки эффективности для неопределенных операций. Разработаны лишь общие требования к критериям и процедурам оценки и выбора оптимальных систем:
1) оптимальное решение не должно меняться с перестановкой строк и столбцов матрицы эффективности,
2) оптимальное решение не должно меняться при добавлении тождественной строки или тождественного столбца к матрице эффективности,
3) оптимальное решение не должно меняться от добавления постоянного числа к значению каждого элемента матрицы эффективности,
4) оптимальное решение не должно становиться неоптимальным, а неоптимальное – оптимальным в случае добавления новых систем, среди которых нет ни одной более эффективной системы,
5) если две системы оптимальны, то их вероятностная смесь тоже должна быть оптимальна.
В зависимости от характера предпочтений ЛПР наиболее часто в неопределенных операциях используются критерии:
ü среднего выигрыша
ü Лапласа
ü осторожного наблюдателя (Вальда)
ü максимакса
ü пессимизма-оптимизма (Гурвица)
ü минимального риска (Сэвиджа).
Критерий среднего выигрыша предполагает задание вероятностей состояний обстановки pi. Эффективность систем оценивается как мат. ожидание оценок эффективности по всем состояниям:
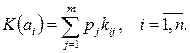
Для оптимальной системы Kopt=max (K (ai)).
Критерий Лапласа предполагает, что т.к. о состояниях обстановки ничего не известно, то они равновероятны. Т.е. это частный случай критерия среднего выигрыша при pj=1/m:
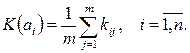Kopt=max (K (ai)).
Критерий осторожного наблюдателя (Вальда) – это максиминный критерий, который гарантирует определенный выигрыш при наихудших условиях, ориентируется на решение, не содержащее риска:
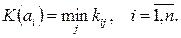
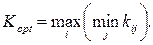
Критерий максимакса – самый оптимистичный из критериев:
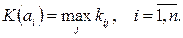
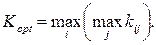
Критерий Гурвица (обобщенного максимина) – вводится коэффициент оптимизма α, вещественное число от 0 до 1 (обычно от 0,3 до 0,7), который отражает склонность ЛПР к риску. При α=0 риск отсутствует, получаем критерий Вальда, при α=1 риск максимален, приходим к критерию максимакса:
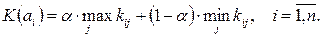
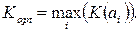
Критерий Сэвиджа – минимизирует потери эффективности при наихудших условиях. На основе матрицы эффективности формируется матрица риска (потерь) по правилу: элемент матрицы риска определяется как разность между максимальным и текущим значениями оценок эффективности в столбце
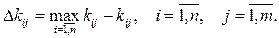
Затем определяется эффективность системы:
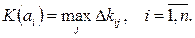
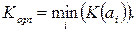
На выбор критерия влияют различные факторы: природа операции и ее цель (иногда допустим риск, иногда необходим гарантированный результат), причины неопределенности, характер ЛПР и его склонность к риску или осторожности.
Пример. Необходимо оценить один из трех вариантов системы ai в неопределенных заранее условиях (обстановке внешней среды) yj. Задана матрица эффективности. Выбрать оптимальный вариант системы, применяя различные критерии.
| ai | yj | Лапласа | Вальда | максимакса | ср. выигрыша | Гурвица | Сэвиджа | |||
| y1 | y2 | y3 | y4 | |||||||
| a1 | 0.1 | 0.5 | 0.1 | 0.2 | 0.225 | 0.1 | 0.5 | 0.21 | 0.34 | 0.3 |
| a2 | 0.2 | 0.3 | 0.2 | 0.4 | 0.275 | 0.2 | 0.4 | 0.28 | 0.32 | 0.2 |
| a3 | 0.1 | 0.4 | 0.4 | 0.3 | 0.3 | 0.1 | 0.4 | 0.25 | 0.34 | 0.1 |
Для критерия среднего выигрыша предположили, что вероятности программных воздействий равны 0.4, 0.2, 0.1, 0.3 соответственно.
Для критерия Гурвица взяли α=0.6.
Для критерия Сэвиджа предварительно вычислена матрица потерь:
| ai | yj | |||
| y1 | y2 | y3 | y4 | |
| a1 | 0.1 | 0.3 | 0.2 | |
| a2 | 0.2 | 0.2 | ||
| a3 | 0.1 | 0.1 | 0.1 |
Тип критерия для выбора рационального варианта должен быть определен на этапе анализа систем, согласован, и в последующих задачах синтеза сложных систем предполагается заданным. Устойчивость выбранного рационального варианта можно оценить на основе анализа по нескольким критериям. Если существует совпадение, то имеется большая уверенность в правильности выбора варианта.
Во всех случаях переход к оценке эффективности систем без введения функции полезности должен всегда сопровождаться обоснованием.
5.3. Принятие решений с помощью дерева решений
Этот процесс предполагает выполнение 5 этапов.
Этап 1. Формулировка задачи. Выделение существенных факторов. Описание задачи в форме, поддающейся анализу. Определение возможностей сбора информации для проведения эксперимента, составление перечня возможных событий с указанием исходов, установление временной последовательности событий и действий, которые можно предпринять.
Этап 2. Построение дерева решений.
Этап 3. Оценка вероятностей состояния среды, т.е. сопоставление шансов возникновения каждого конкретного события из статистики либо экспертным путем).
Этап 4. Установление выигрышей (проигрышей) для каждой возможной комбинации альтернатив и состояний среды.
Этап 5. Решение задачи.
Рассмотрим на примере анализа рыночного поведения с помощью аппарата игр.
На рынке некоторого продукта доминирует монополист Фирма 1 и получает 12 млрд.руб. прибыли. Фирма 2 привлечена высокой прибылью в данном секторе, и она решает вопрос: «Построить завод по производству такого же продукта или нет?» Однако ей известно, что Фирма 1 может либо снизить объем своего производства, либо сохранить прежний объем. В зависимости от решений прибыли фирм можно представить в виде матрицы (первое число – прибыль Фирмы 1).
| Выигрыши в млрд.руб. | Стратегии Фирмы 2 | ||
| сохранить | снизить | ||
| Стратегии Фирмы 2 | вступить | 5; -2 | 6; 6 |
| воздержаться | 12; 0 | 8; 0 |
Однако в отличие от классических биматричных игр фирмы принимают решения не одновременно. Игра является позиционной. Первый ход за Ф2 (рис.5.1).
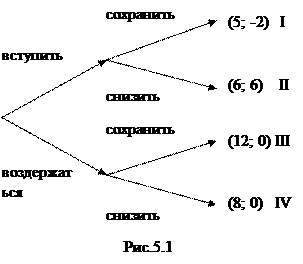Вершины дерева (графа) – позиции игры. Пути, ведущие в окончательные позиции, являются партиями. Внутренние вершины – альтернативные.
Имеем две ситуации равновесия по Нэшу: (12; 0) и (6; 6). Но Ф1 принимает решение, уже зная решение Ф2. Если Ф2 придерживается максиминной стратегии, то выберет (12; 0). Но одна из главных предпосылок теории игр – рациональность поведения игроков, стремящихся к максимизации своих выигрышей. Насколько вероятна реализация Фирмой 1 стратегии (угрозы) «сохранить объем производства» при вступлении Ф2 в рынок? В этом случае прибыль Ф1 составит 5 млрд.руб., что меньше 6 млрд.руб, которые она получит, если разделит рынок с Ф2. В данных (численных) условиях угроза Ф1 сохранить объем производства в ответ на вторжение Ф2 на рынок является неправдоподобной. Ситуация (6; 6) является не только равновесной по Нэшу, но и учитывает степень правдоподобности угрозы.
При изменении численных условий задачи может возникнуть ситуация устойчивой монополии, когда фирма-монополист в состоянии эффективно реализовать угрозу подавления своих потенциальных партнеров (рис.5.2). Это может объясняться естественными условиями производства, его технологическими особенностями, факторами, позволяющими фирме -монополисту гибко реагировать на действия противников (большой запас мощностей, реклама, вложения в перспективные исследования и т.п.). Следовательно, у государственных органов существует желание и контролировать, и ограничивать деятельность подобных устойчивых монополистов для развития рынка.
Лекция 6 МЕТОД АНАЛИЗА ИЕРАРХИЙ
Метод анализа иерархий является систематической процедурой для иерархического представления элементов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена численно относительная степень (интенсивность) взаимодействия элементов в иерархии. Метод анализа иерархии включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Полученные таким образом значения являются оценками в шкале отношений.
Метод основан на применении следующих принципов: идентичности и декомпозиции, дискриминации, сравнительного суждения и синтезирования:
6.1. Принцип идентичности и декомпозиции
Принцип идентичности и декомпозиции предусматривает структурирование проблем в виде иерархии или сети, что является первым этапом применения МАИ. В наиболее элементарном виде иерархия строится с вершины (целей — с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем альтернатив).
Существует несколько видов иерархий. Самые простые — доминантные иерархии, которые похожи на перевернутое дерево с основой в вершине. Холлархии — это по существу доминантные иерархии с обратной связью. Китайский ящик (или модулярные иерархии) растет в размерах от простейших элементов или компонент (внутренние ящики) ко все более крупным совокупностям (внешние ящики). В биологии интерес представляют неогенетические иерархии, в которых новые верхние уровни возникают последовательно в течение эволюции. Мы сконцентрируем внимание на доминантных иерархиях, хотя теория, описанная ниже, распространяется и на другие иерархические формы. Иерархия считается полной, если каждый элемент заданного уровня функционирует как критерий для всех элементов нижестоящего уровня.
Такая форма нисходящей декомпозиции может быть использована для задач широкого класса. Несложная модификация с включением петель обратной связи охватит еще более широкий класс задач. Закон иерархической непрерывности требует, чтобы элементы нижнего уровня иерархии были сравнимы попарно по отношению к элементам следующего уровня и т.д. вплоть до вершины иерархии.
