Преобразования в трехмерном пространстве

Примечания

1. В общем случае от перемены матриц местами результат меняется.
2. Матрицы операций, идущие подряд, можно перемножать раздельно, главное — не менять их порядок следования (см. примечание 1).
3. Линии при описанных выше (аффинных) преобразованиях переходят в линии. Поэтому обычно производится пересчет только координат вершин фигуры, а после этого соответствующие вершины в результирующей фигуре соединяются, как и в исходной фигуре.

Нахождение точки пересечения двух линий (пример)

Пусть имеются две линии: x + y = 1, 2x - 3y = 0, необходимо найти точку их пересечения. Решение может быть найдено с использованием матриц. Перенесем все члены уравнений в левую часть: x + y - 1 = 0, 2x - 3y - 0 = 0; запишем коэффициенты первого уравнения в первый столбец матрицы, второго уравнения — во второй:

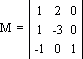
Условие, при котором пересекаются две прямые, выглядит следующим образом:
|x y 1| * M = |0 0 1|

Для нахождения ответа необходимо обе части предыдущего уравнения домножить справа на обратную матрицу M^-1 (при перемножении M и M^-1 получается единичная матрица E):
|x y 1| * E = |0 0 1| * M^-1

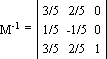
|x y 1| = |3/5 2/5 1|

Ответ: точка пересечения прямых: x = 3/5, y = 2/5.

Выше были рассмотрены операции, которые можно выполнять с точкой на плоскости. Такие же операции имеются и в трехмерном пространстве. Отличие здесь небольшое: точка задается не двумя, а тремя координатами, и при работе в однородных координатах матрицы преобразований/операций будут состоять не из трех, а из четырех столбцов.