ОБЩИЕ СВОЙСТВА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
задача об использовании оборудования.
Предприятие выпускает два вида изделий А и В, для производства которых используются три типа станков. Известны затраты времени (в часах) станками на производство единицы каждого вида изделий, резервы времени станков, а также прибыль от реализации каждого вида изделия. Все эти данные приведены в таблице:
| Изделия станки | А | В | Резервы времени (в часах) |
| I | Затраты времени на пр-во ед. изделия (в часах) | ||
| II | |||
| III | |||
| Прибыль от реализации ед. изделия |
Требуется составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Это пример оптимизационной экономической задачи. Решение таких задач включает в себя следующие этапы:
построение экономико-математической модели;
решение полученной математической задачи каким-либо математическим методом;
внедрение результата решения в практику.
Под экономико-математической моделью понимается система математических соотношений, описывающих экономический процесс.
Построим экономико-математическую модель задачи об использовании оборудования.
Пусть х1 - количество изделий А, а  - количество изделий В, которые будут выпущены предприятием. Тогда прибыль,полученная предприятием, будет равна
- количество изделий В, которые будут выпущены предприятием. Тогда прибыль,полученная предприятием, будет равна 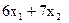 , Переменные
, Переменные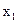 и
и  нужно подобрать так, чтобы функция
нужно подобрать так, чтобы функция  максимизировалась. Так как первый станок может работать не более 30 часов, то должно выполняться соотношение
максимизировалась. Так как первый станок может работать не более 30 часов, то должно выполняться соотношение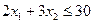 . Аналогичные ограничения на переменные х1 и х2 накладываются резервами времени второго и третьего станков. Учитывая еще, что переменные х1 и х2 могут принимать только неотрицательные значения, получим следующую экономико-математическую модель задачи:
. Аналогичные ограничения на переменные х1 и х2 накладываются резервами времени второго и третьего станков. Учитывая еще, что переменные х1 и х2 могут принимать только неотрицательные значения, получим следующую экономико-математическую модель задачи:

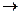 max
max
при ограничениях
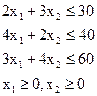
2.2. Задача об использовании сырья.
С математической точки зрения эта задача является обобщением той, которая рассмотрена в предыдущем параграфе. Формулируется она так.
Предприятие выпускает продукцию n видов 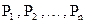 , на изготовление которой расходуется сырье m видов
, на изготовление которой расходуется сырье m видов 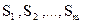 , запасы которого на предприятии равны соответственно
, запасы которого на предприятии равны соответственно 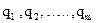 . Известны расходы
. Известны расходы 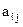 сырья Si на производство единицы продукции
сырья Si на производство единицы продукции 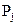 (i =
(i = 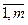 ; j =
; j = ). Стоимость единицы продукции
). Стоимость единицы продукции 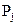 равна
равна 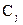 (j =
(j = ). Требуется составить такой план выпуска продукции, при котором выручка от реализации продукции была бы наибольшей.
). Требуется составить такой план выпуска продукции, при котором выручка от реализации продукции была бы наибольшей.
Составим математическую модель задачи.
Пусть  - количество единиц продукции
- количество единиц продукции 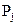 (j =
(j = ).
).
Математическая модель имеет вид:
f =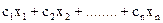 → max
→ max
при ограничениях:
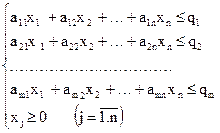 (2.0)
(2.0)
 2014-02-04
2014-02-04 609
609








