Двойственность в линейном программировании

Таблица 3.21

Таблица 3.20

Таблица 3.18

Таблица 3.17

Таблица 3.16

Таблица 3.15

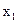
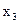
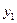
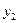
Б						Q
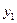
		-1
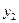
	-2
F	-1

Перейдем к новой симплекс-таблице (таблица 3.16)

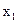
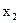
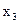
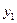
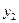
Б						Q
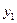
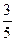
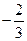
F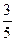

Переходим к следующей симплекс-таблице. Обратим внимание, что в качестве генерального столбца взят первый, а не третий столбец - это наше право!

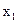
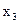
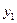
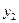
Б						Q
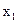
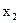
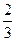
F				-1	-1

Мы достигли оптимального плана для вспомогательной задачи; при этом 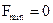. Выпишем жорданову форму, соответствующую таблице 3.17:

Опустив искусственные переменные, получим жорданову форму с неотрицательными правыми частями для исходной задачи:

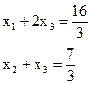
Теперь приступаем к решению исходной задачи. Приведем ее к табличному виду

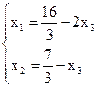
Составим симплекс-таблицу для исходной задачи (таблица 3.18) и переходим к следующей таблице 3.19

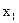
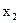
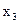
Б				Q
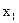
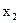
F

Таблица 3.19

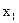
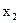
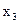
Б				Q
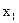
		-2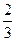
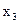
F		-1		-1

Получим оптимальное решение:

С целью частичного контроля правильности вычислений можно убедиться в том, что полученное решение является допустимым решением исходной задачи, значение целевой функции при котором равно -1.

Пример 2. Решить симплекс-методом

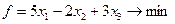
Составим вспомогательную задачу

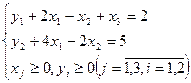
Известными приемами приведем ее к табличному виду:

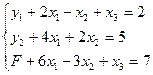
Заполним симплекс-таблицу (таблица 3.20)

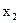
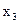
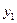
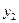
Б						Q
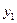
		-1
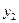
		-2
F		-3

Перейдем к новой симплекс-таблице (3.21)

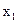
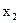
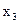
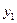
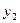
Б						Q
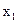
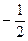
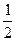
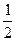
			-2	-2
F			-2	-3

Получим оптимальный план. Значение целевой функции при оптимальном плане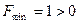. Поэтому исходная ЗЛП неразрешима из-за пустоты ОДР.

Любопытно отметить, что система линейных уравнений исходной ЗЛП совместна и приводится к жордановой форме. Однако она не приводится к жордановой форме с неотрицательными правыми частями.

Сделаем еще одно полезное замечание. В рассматриваемом примере 2 можно было бы составить более простую вспомогательную задачу:

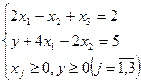
Дело в том, что цель введения искусственных переменных - получение жордановой формы с неотрицательными правыми частями для вспомогательной задачи. Здесь эта цель достигается с помощью одной искусственной переменной у. Допустимый базис состоит из переменных 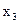и у.

3.8. Вырожденность опорного плана. Зацикливание.

Опорный план ЗЛП называется вырожденным, если некоторые из базисных переменных принимают значение 0. В этом случае при переходе от одного плана к другому может не произойти уменьшения целевой функции.

Пример. Пусть табличный вид ЗЛП таков:

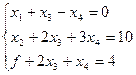
Составим первую симплекс-таблицу (таблица 3.22).

Таблица 3.22

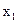
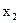
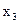
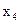
Б					Q
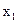
				-1
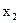
f

Опорный план, соответствующий этой симплекс-таблице, является вырожденным, так как значение базисной переменной 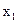равно 0. Перейдем к новой симплекс-таблице (табл.3.23)

Таблица 3.23

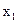
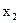
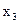
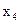
Б					Q
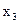
				-1
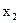
	-2
f	-2

При новом опорном плане значение целевой функции осталось прежним: f=4.

При вырожденных опорных планах возможна ситуация, когда, последовательно переходя от одного опорного плана к другому, через определенное количество шагов можно вернуться к прежнему опорному плану, так и не достигнув минимума функции. Это называется зацикливанием.

На практике зацикливание встречается крайне редко. Существует такая модификация симплекс-алгоритма, при которой зацикливание исключается. Для практических целей достаточна и следующая рекомендация: если произошло зацикливание, то при первой же возможности нужно иначе выбрать генеральный элемент, нежели это делалось в первый раз.

Справедлива теорема о конечности симплекс-алгоритма: если ЗЛП разрешима, то оптимальное решение всегда может быть найдено с помощью симплекс-метода, причем начинать можно с любого опорного плана.