Различают:
1) мгновенная мощность: 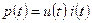 ,
,
2) полная мощность: 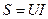 ,
,
3) активная мощность: 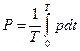 ,
,
4) реактивная мощность: 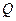 .
.
Способ расчёта потребляемой и генерируемой мощности такой же как и всегда.
Если u(t) и i(t) представлены в виде рядов Фурье: 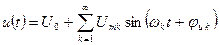 ,
, 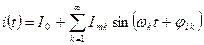 , то можно упростить вычисление активной мощности.
, то можно упростить вычисление активной мощности.
Перемножим записанные ряды; получим три вида слагаемых:
1) 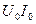 ;
;
2) 
где k одно и то же;
3) произведение гармоник с разными номерами.
При интегрировании за период Т – каждое слагаемое третьего типа даёт ноль. Интеграл от слагаемого второго типа будет давать 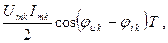 т.к. интеграл от
т.к. интеграл от 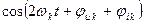 за период равен нулю. Слагаемое первого типа даст
за период равен нулю. Слагаемое первого типа даст 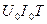 .
.
В результате получим, что
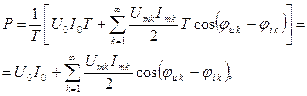
т.е. фактически активная мощность периодического несинусоидального тока равна сумме активных мощностей всех гармоник, начиная с нулевой.
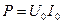 ,
,  ,
,
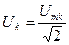 ,
, 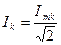 .
.
По аналогии вводится реактивная мощность, только вместо cos будет sin, и не будет учитываться нулевая гармоника:
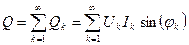 .
.
 2014-02-04
2014-02-04 405
405








