2014-02-05
408
2 основных свойства:
1. гидростатическое давление всегда направлено по внутренней нормали к рассматриваемой площадке
2. гидростатическое давление в точке не зависит от ориентации площадки, по которой оно действует.
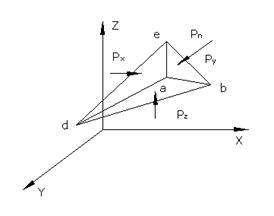
Пренебрегая массовыми силами, запишем уравнение равновесия
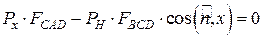
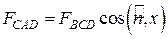
Так как размеры тетраэдра и положение его граней выбраны произвольно, то при стягивании тетраэдра в точку давление в ней по всем направлениям будет одинаково.
Дифференциальное уравнение равновесия жидкости (уравнение Эйлера).
Рассмотрим равновесие жидкости, покоящейся в силовом поле, единичная массовая сила которого в проекции на оси координат = X, Y, Z.
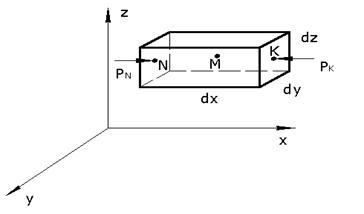
Пусть давление в точке М – Р. При переход из точки М в точку N координата x изменится на dx.
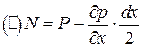
Уравнение равновесия.
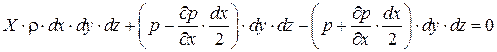
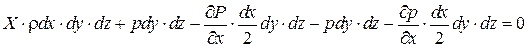
Разделим на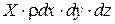 
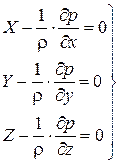
суммируя эти уравнения, получим
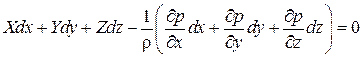
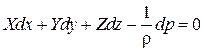
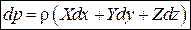- уравнение Эйлера
Изменение давления определяется плотностью, единичными массовыми силами, действующими на жидкость, и изменением координаты. Уравнение Эйлера справедливо как для жидкостей, так и для газов.
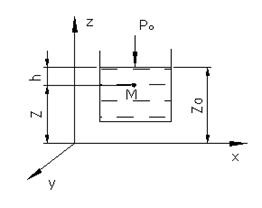
Рассмотрим равновесие жидкости, находящейся в пол сил тяжести.
X=0 Y=0 Z=-g
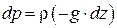
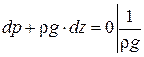
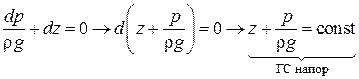
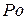- давление на поверхности жидкости
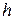- заглубление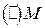 
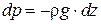
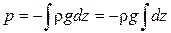
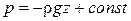
Найдем const из граничных условий: при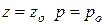 
- основное уравнение гидростатики
Давление, приложенное к внешней поверхности жидкости, передается всем точкам жидкости и по всем направления одинаково (закон Паскаля).
Из анализа уравнения следует:
1. Давление в точке зависит от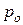 
, плотности, единичной массовой силы и глубины погружения точки от свободной поверхности.
2. Закон изменения давления по вертикали - линейный.
