Как и в случае ламинарного движения, изучение турбулентного движения в трубе сводится к выяснению характера распределения скорости по сечению трубы и к установлению закона сопротивления движению. Полагая суммарное напряжение в рассматриваемом потоке величиной постоянной и принимая гипотезу Прандтля для турбулентных напряжений, запишем уравнение (5.38) в виде
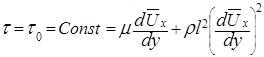 . (5.43)
. (5.43)
Опыты показывают, что по мере приближения к стенке турбулентные пульсации затухают, следовательно, уменьшается величина  и в непосредственной близости от стенки становится ничтожно малой по сравнению с
и в непосредственной близости от стенки становится ничтожно малой по сравнению с 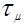 , так что в пределах пристеночного слоя можно принять
, так что в пределах пристеночного слоя можно принять 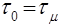 .
.
По мере удаления от стенки роль турбулентных пульсаций возрастает и, начиная с некоторого расстояния, величина 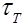 во много раз превосходит величину
во много раз превосходит величину 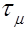 так, что для этой области потока можно принять
так, что для этой области потока можно принять 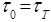 .
.
Для пристеночной области потока, часто именуемой ламинарным подслоем,
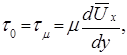 (5.44)
(5.44)
где 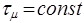 –напряжение трения на стенке трубы.
–напряжение трения на стенке трубы.
Откуда 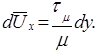
Интегрируя последнее уравнение, получим
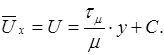
При 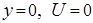 постоянная интегрирования С=0. В ламинарном подслое распределение скорости носит линейный характер:
постоянная интегрирования С=0. В ламинарном подслое распределение скорости носит линейный характер:
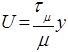 . (5.45)
. (5.45)
Обратимся теперь к области турбулентного течения, для которого
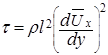 . (5.46)
. (5.46)
Используя для длины пути перемешивания 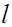 формулу Прандтля
формулу Прандтля
l= ϰ y, получим
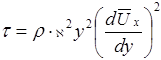 , (5.47)
, (5.47)
откуда
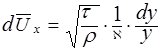 . (5.48)
. (5.48)
Обозначая
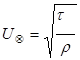
и интегрируя уравнение (5.48), находим
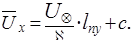 (5.49)
(5.49)
Для определения произвольной С следует в данном случае привлечь условие, относящееся к границе раздела между турбулентным ядром потока и ламинарным подслоем, где
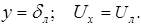
Здесь 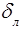 –толщина ламинарного подслоя, а
–толщина ламинарного подслоя, а 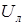 –скорость на его границе.
–скорость на его границе.
Записывая уравнение (5.50) для границы ламинарного подслоя, получим
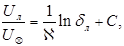
откуда
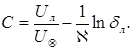 (5.50)
(5.50)
Исходя из уравнения (44) для границы ламинарного подслоя, можно написать
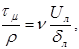 так как
так как 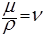 .
.
С учетом скорости 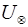 выражение для
выражение для 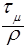 можно представить в виде
можно представить в виде
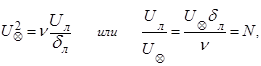 (5.51)
(5.51)
откуда толщина ламинарного подслоя
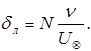 (5.52)
(5.52)
Подставляя значение 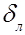 из (51) в (49), получим
из (51) в (49), получим
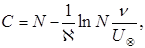 (5.53)
(5.53)
а подставляя (5.53) в (5.48), имеем
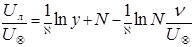 ,
,
или
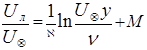 ,
,
где 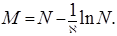
Коэффициенты 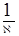 и
и  можно определить опытным путем. Так, в результате опытов Никурадзе получена формула, определяющая распределение скоростей в гладких трубах, в виде
можно определить опытным путем. Так, в результате опытов Никурадзе получена формула, определяющая распределение скоростей в гладких трубах, в виде
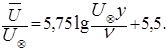 (5.54)
(5.54)
Это уравнение выражает универсальный логарифмический закон распределения скоростей.
Полагая в уравнении (5.54) 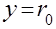 , найдем скорость на оси трубы (
, найдем скорость на оси трубы (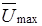 ):
):
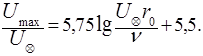 (5.55)
(5.55)
Зная закон распределения скоростей, можно найти величину коэффициента гидравлического трения. Для гидравлических гладких труб, исходя из формулы (5.54) для средней скорости потока, можно записать
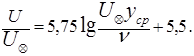 (5.56)
(5.56)
где 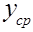 =0,223
=0,223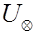 –расстояние от стенки до слоя, в котором скорость равна средней скорости U.
–расстояние от стенки до слоя, в котором скорость равна средней скорости U.
Выше была получена зависимость
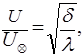
подставляя которую в (5.56), найдем
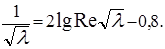 (5.57)
(5.57)
Это известная формула Прандтля для коэффициента гидравлического трения в гладких трубах. Недостаток этой формулы заключается в том, что в ней зависимость 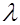 от числа Re выражена в неявной форме, поэтому решать её приходится методом последовательных приближений. От этого недостатка свободна эмпирическая формула Конакова
от числа Re выражена в неявной форме, поэтому решать её приходится методом последовательных приближений. От этого недостатка свободна эмпирическая формула Конакова
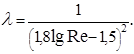 (5.58)
(5.58)
Наряду с логарифмическими формулами для коэффициента сопротивления трубы и для распределения скорости при турбулентном движении существуют степенные, однако, они менее универсальны. Так, широкое применение получила эмпирическая формула Блазиуса, пригодная при значениях числа Рейнольдса, не превышающих 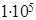 :
:
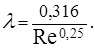 (5.59)
(5.59)
Этой формуле отвечает степенное выражение для распределения скорости потока по сечению трубы, область применения которого также ограничивается указанным значением числа Рейнольдса:
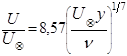 , (5.60)
, (5.60)
где у –расстояние от стенки трубы.
Это уравнение известно под названием закона Блазиуса.
Для максимальной скорости на оси трубы (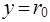 )
)
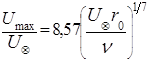 . (5.61)
. (5.61)
Из равенств (5.30) и (5.31) получим
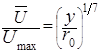 .
.
 2014-02-05
2014-02-05 1186
1186








