Истечение жидкости через малые отверстия
СВОБОДНЫЕ СТРУИ
ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДКОВ.
В практической деятельности часто приходится сталкиваться с различными случаями истечения жидкости из отверстий и протеканием ее через патрубки, называемые насадками (в эжекторах, т.е. водоструйных насосах, в гидромониторах, гидротурбинах, карбюраторах, пожарных устройствах, при опорожнении различных емкостей и т.д.).
При истечении жидкости через отверстие, сделанное в боковой стенке или дне сосуда, вся жидкость, находящаяся в нем, приходит в движение. Однако потери напора в сосуде будут ничтожны. Поэтому скорость подхода 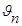 (рис.1), т.е. средняя скорость в «подходном» плоском живом сечении 1–1 будет также незначительной. Обозначим через
(рис.1), т.е. средняя скорость в «подходном» плоском живом сечении 1–1 будет также незначительной. Обозначим через 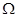 площадь «подходного» живого сечения 1–1, а через
площадь «подходного» живого сечения 1–1, а через 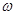 –площадь отверстия. В случае, если
–площадь отверстия. В случае, если 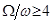 , скоростью подхода можно пренебрегать, так как ошибка при этом будет менее 5%.
, скоростью подхода можно пренебрегать, так как ошибка при этом будет менее 5%.
Тогда можно считать, что
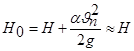 .
.

Рис.1
Основным вопросом при изучении истечения жидкости из отверстий и насадков является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Рассмотрим случай истечения жидкости через малое отверстие в тонкой стенке (рис.1). Малым будем называть отверстие, которое одновременно удовлетворяет двум условиям:
1) скорость подхода пренебрежимо мала, т.е. соблюдается неравенство 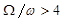 ;
;
2) скорости 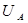 и
и 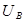 (в верхней и нижней точках сжатого живого сечения) примерно равны друг другу, т.е.
(в верхней и нижней точках сжатого живого сечения) примерно равны друг другу, т.е. 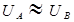 (это наблюдается когда
(это наблюдается когда 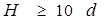 , где d –высота отверстия).
, где d –высота отверстия).
Под тонкой стенкой понимается такая стенка, у которой края отверстия имеют заостренную кромку. При этом кромка заострена так, что вытекающая из отверстия струя касается стенки по одной линии. В этом случае возможны только местные сопротивления движению жидкости.
Сжатие струи от 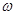 до
до 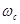 обусловлены инерцией частиц жидкости, движущихся при подходе к отверстию по различным криволинейным траекториям.
обусловлены инерцией частиц жидкости, движущихся при подходе к отверстию по различным криволинейным траекториям.
На пути от выхода из отверстия до сжатого сечения С–С движение резко изменяющееся, а после него – плавно изменяющееся.
Сжатое сечение С–С является первым (после выхода из отверстия) сечением, к которому можно применить уравнение Бернулли, так как линии тока в сжатом сечении близки к параллельном прямым, а скорости здесь распределяются примерно равномерно и эпюра скоростей близка к прямоугольнику.
Введем обозначение
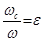 , (6.1)
, (6.1)
где 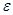 – коэффициент сжатия струи.
– коэффициент сжатия струи.
Найдем среднюю скорость 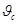 в сжатом сечении и расход Q жидкости, вытекающей из сосуда. Для решения этой задачи соединим уравнением Бернулли сечения 1–1 и 2–2, первое из которых совпадает с поверхностью жидкости в сосуде (подходное сечение), а второе проходит через сжатое сечение С–С. Плоскость сравнения 0–0 проведем через центр тяжести сечения С–С:
в сжатом сечении и расход Q жидкости, вытекающей из сосуда. Для решения этой задачи соединим уравнением Бернулли сечения 1–1 и 2–2, первое из которых совпадает с поверхностью жидкости в сосуде (подходное сечение), а второе проходит через сжатое сечение С–С. Плоскость сравнения 0–0 проведем через центр тяжести сечения С–С:
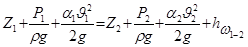 ,
,
где
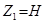 ;
; 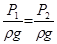 ;
; 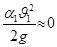 ;
; 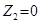 ;
;
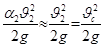 ;
; 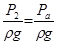 ;
; 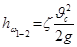 .
.
 –коэффициент сопротивления, учитывающий потери полного напора от сечения 1–1 до сечения 2–2.
–коэффициент сопротивления, учитывающий потери полного напора от сечения 1–1 до сечения 2–2.
Следует иметь в виду, что потери напора сосредотачиваются в основном в районе самого отверстия, где скорости уже достаточно велики:
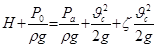 . (6.2)
. (6.2)
Обозначим
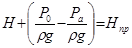 , (6.3)
, (6.3)
где 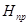 –приведенный напор.
–приведенный напор.
Тогда
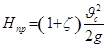 , (6.4)
, (6.4)
откуда
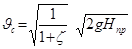 , (6.5)
, (6.5)
или
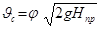 , (6.6)
, (6.6)
где 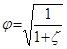 –коэффициент, учитывающий потери напора и называемый коэффициентом скорости.
–коэффициент, учитывающий потери напора и называемый коэффициентом скорости.
При 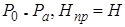 , следовательно,
, следовательно,
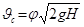 . (6.7)
. (6.7)
Для идеальной жидкости
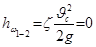 ,
,
т.е. в этом случае 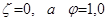 .
.
Следовательно, для идеальной жидкости
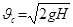 . (6.8)
. (6.8)
Эта формула называется формулой Торичелли.
Зная скорость 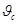 в сжатом сечении, найдем расход Q для случая
в сжатом сечении, найдем расход Q для случая 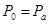 . Очевидно, что
. Очевидно, что

или окончательно
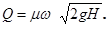 (6.9)
(6.9)
Для круглых и квадратичных отверстий (по опытным данным) для квадратичной области сопротивления:
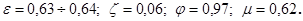
В случае истечения жидкости под уровень (случай затопленного отверстия) в формуле для расхода (6.9) вместо H подставляется Z –разность уровней жидкости в сосудах (рис.2).
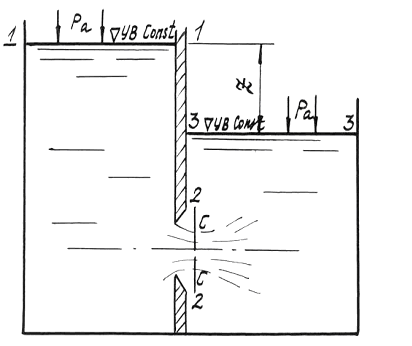
Рис.2
 ,
,
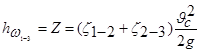 ,
,
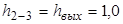 .
.
 2014-02-05
2014-02-05 996
996








