Рис.6
Последнюю зависимость можно прочитать так: для сходственных точек всех поперечных сечений отношение 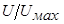 есть величина постоянная:
есть величина постоянная:
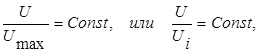
где 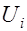 –скорость в произвольной точке сечения струи.
–скорость в произвольной точке сечения струи.
Однако это подобие эпюр скоростей не следует понимать как простое геометрическое подобие между ними. Это подобие представляет собой некоторое однообразие в форме эпюры. Оно заключается, по существу, в одной и той же закономерности распределения скоростей во всех сечениях основного участка струи. В связи с этим, если известны эпюра скоростей и закономерность изменения скорости в какой-либо характерной точке сечения, например в осевой точке 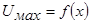 , то этим полностью определяется все поле скоростей струи.
, то этим полностью определяется все поле скоростей струи.
Г.Н. Абрамович дает следующее уравнение осевой скорости для круглой струи:
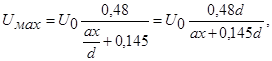 (6.19)
(6.19)
где x – расстояние от «полюса» до рассматриваемого сечения струи; d –диаметр выходного отверстия; a –коэффициент турбулентности или коэффициент структуры, учитывающий структуру потока в выходном сечении.
Для практических расчетов можно принимать a =0,08.
Все параметры круглой струи определяются по формулам
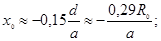 (6.20)
(6.20)
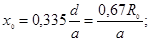 (6.21)
(6.21)
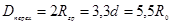 ; (6.22)
; (6.22)
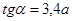 . (6.23)
. (6.23)
В этой струе можно выделить три характерные части: компактную, раздробленную и распыленную (рис.7).
В пределах компактной части струя сохраняет цилиндрическую форму, а сплошность потока еще не нарушается. В пределах раздробленной части сплошность струи нарушается, причем наблюдается ее постепенное расширение. Наконец, в пределах распыленной части струи происходит распад потока на отдельные капли. Разрушение струи, т.е. ее раздробление, а затем и распыление, объясняется аэрацией струи. Аэрация же, в свою очередь, обусловливается действием сил собственного веса жидкости и сил сопротивления воздуха, вызывающих турбулентный обмен частиц через границу между воздушной и водяной средами.
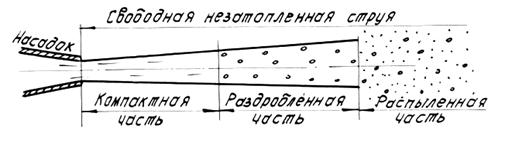
Рис.7
Уравнение теоретической траектории свободной струи выводится из предположения, что все частицы движутся совершенно одинаково, причем каждая, как свободная материальная точка в пустоте. В этом случае уравнение траектории (рис.8) в параметрической форме может быть представлено в виде:
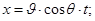 (6.24)
(6.24)
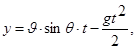 (6.25)
(6.25)
где 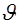 –начальная скорость;
–начальная скорость; 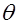 –угол наклона вектора начальной скорости к горизонту;
–угол наклона вектора начальной скорости к горизонту; 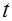 –время.
–время.
Исключая время, получим
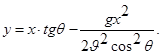 (6.26)
(6.26)
Полагая в последней формуле y=0, определим 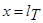 –теоретическую дальность полета струи (дальность боя), откуда следует, что теоретическая максимальная дальность боя будет при
–теоретическую дальность полета струи (дальность боя), откуда следует, что теоретическая максимальная дальность боя будет при 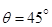
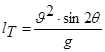 , (6.27)
, (6.27)
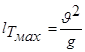 . (6.28)
. (6.28)

 2014-02-05
2014-02-05 1881
1881








