2014-02-05
530
Рис. 2.3
Рис. 2.2
Рис. 2.1
Аналогично:
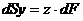(2.2)
Просуммировав такие произведения по всей площади фигуры, получим соответственно статические моменты относительно осей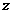 
и 
:
; 
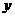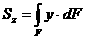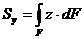(2.3)
Пусть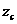 
, 
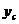- координаты центра тяжести фигуры. Продолжая аналогию с моментами сил, на основании теоремы о моменте равнодействующей можно написать следующие выражения:
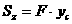
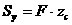(2.4)
где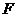 
- площадь фигуры. Очевидно, что статические моменты площади относительно осей проходящих через центр тяжести (центральных осей) равны нулю.
Координаты центра тяжести:
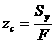
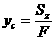. (2.5)
В качестве примера вычислим статический момент треугольника (рис. 2.2) относительно оси, проходящей через основание. На расстоянии 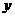от нее выделим элементарную площадку в виде полоски, параллельной оси 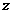. Площадь полоски
.
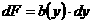Учитывая, что
,
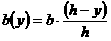имеем
.
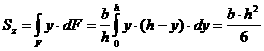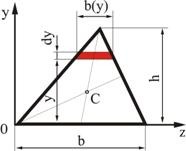
Еще проще решить эту задачу, пользуясь формулой (2.4).
Учитывая, что
; 
,
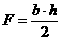статический момент
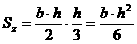
Для вычисления статических моментов сложной фигуры ее разбивают на простые части (рис. 2.3), для каждой из которых известна площадь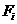 
и положение центра тяжест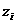и 
и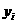 
. Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:
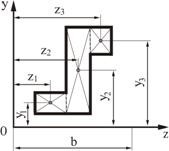
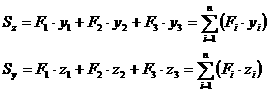(2.6)
По формулам (2.5) и (2.6) легко найти координаты центра тяжести сложной фигуры:
; 
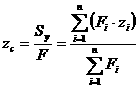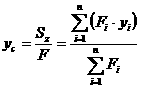(2.7)
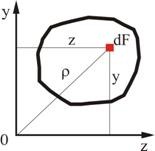
Осевым, или экваториальным, моментом инерции площади фигуры называют интеграл произведений элементарных площадей на квадраты расстояний от рассматриваемой оси
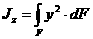
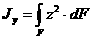(2.8)
