Как реагирует система на единичный скачок?

Контрольные вопросы.

Рис.5.102.Переходный процесс для квадратичной интегральной оценки

Рис.5.101.Графики для интегральной оценки

Рис.5.100.Логарифмическая амплитудно-частотная характеристика

Рис.5.99.Переходная функция

Рис.5.97.АФХ разомкнутой системы

Рис.5.96.Построение переходного процесса для астатической системы

Рис.5.95.Построение переходного процесса для статической системы

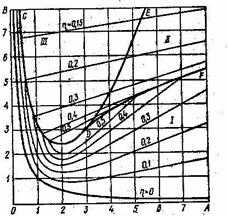
Рис.5.85. Диаграмма Вышнеградского

Частотные методы анализа качества процесса регулирования. Используя преобразование Лапласа и интеграл Фурье, можно установить связь между переходным процессом и частотными характеристиками системы. Га этом основан частотный метод анализа качества процесса регулирования.

Графо-аналитическое определение вещественной частотной характеристики или мнимой частотной характеристики замкнутой системы может быть осуществлено, если известны частотные характеристики разомкнутой системы.

Рассмотрим способ определения вещественной 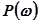и мнимой 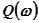характеристик замкнутой системы по АФХ разомкнутой системы, предложенный В.В. Солодовниковым.

Между АФХ разомкнутой 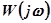и замкнутой 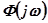систем связь, определяемая зависимостью 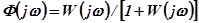, где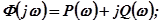

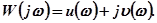
Выделяя в первом уравнении вещественную и мнимую части слева и справа, а затем приравнивая отдельно вещественные т мнимые части, найдём:

;

.

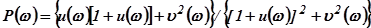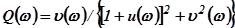Соотношения этих уравнений выражают вещественную и мнимую частотные характеристики замкнутой системы через координаты 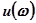и 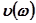АФХ разомкнутой системы. Эти выражения позволяют найти в плоскости 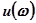, 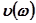геометрические места точек, соответствующие постоянным значениям вещественной 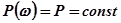и мнимой 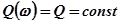характеристик. Тогда последние формулы после несложных преобразований могут быть приведены к виду

,

.

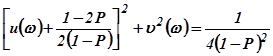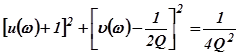Первое из этих двух уравнений показывает, что геометрическое место точек равных 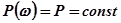на плоскости 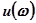, 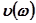определяется окружностью, центр которой находится на оси 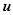и удалён от начала координат на величину, равную абсциссе 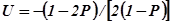, а радиус .

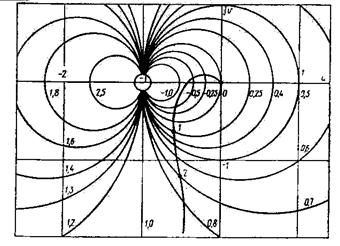Рис.5.86.АФХ разомкнутой системы

На основании этих уравнений могут быть построены окружности для различных постоянных значений 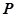. На рис.5.86 приведены их конкретные числовые величины. Все окружности проходят через точку -1 на оси 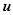. Окружность соответствующая 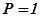, имеет бесконечно большой радиус. Она определяется прямой, параллельной оси ординат и расположенной слева от неё на расстоянии, равном единице. Окружности, находящиеся слева от этой прямой, соответствуют 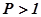. Окружности, расположенные справа от прямой имеют 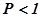. Все окружности для 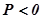располагаются внутри окружности, проходящей через начало координат и точку -1 на оси 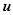и соответствующей 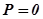. Диаграммы, представленные на рис.5.86, называются круговыми.

Процесс определения вещественной частотной характеристики с использованием круговой диаграммы весьма прост. В координатах диаграммы строится АФХ разомкнутой системы (участок кривой 1-2 на рис.5.86) и рассматриваются её пересечения с окружностями. Каждая точка пересечения соответствует определённой частоте, которая устанавливается по АФХ, и ординате вещественной частотной характеристики при этой частоте, равной индексу окружности. Пусть, например, для точки пересечения 2 частота имеет значение 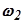. Тогда ордината вещественной характеристики 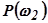равна индексу окружности 0,7, т.е. 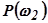=0,7.

Из уравнения 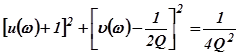следует, что геометрическим местом точек равных значений 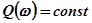на плоскости 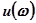, 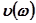будет окружность, центр которой располагается на прямой 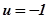, а радиус .

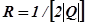Семейство окружностей (по приведённому выше уравнению) показано нарис.5.87. Методика определения мнимой частотной характеристики 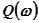по АФХ разомкнутой системы аналогична методика определения .

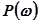Построение вещественной частотной характеристики по логарифмическим частотным характеристикам разомкнутой системы.

Вещественная частотная характеристика замкнутой системы может быть определена по логарифмическим частотным характеристикам разомкнутой системы.

Представим выражение 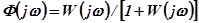в виде

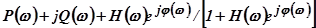
Учитывая, что

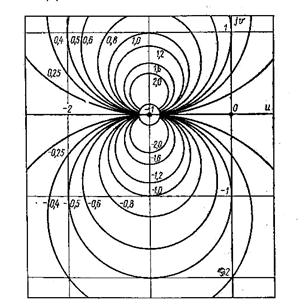
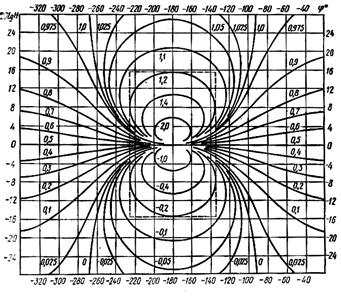Рис.5.87.Семейство окружностей Рис.5.88.Семейство линий равных значений Р

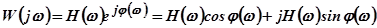, получим:

.

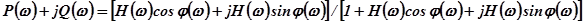Из этого уравнения находим:

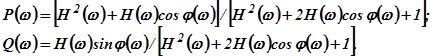
Первое из этих выражений позволяет определить геометрическое место точек, соответствующее равным значениям вещественной характеристики 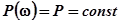в координатах плоскости, где по одной из осей откладывается усиление 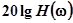, а по другой – фаза 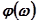разомкнутой системы. Семейство линий равных значений Р показано на рис.5.88.

Если заданы логарифмические АЧХ и ФЧХ разомкнутой системы, то, перенося значения амплитуды и фазы при различных частотах на плоскость номограммы (рис.5.88), получим АФХ разомкнутой системы в координатах номограммы. Точки пересечения этой характеристики с линиями равных значений Р определяют частоту и соответствующую ординату вещественной характеристики 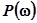, равной индексу кривой номограммы, на которой лежит рассматриваемая точка пересечения.

Для грубой оценки корней типового характеристического уравнения высокого порядка 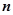, где 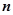- чётное число, часто удобно снизить этот порядок на «2» нахождением приближённого значения множителя в виде квадратного полинома. Для этого левую часть исходного уравнения делят на коэффициент при высшей степени 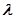и приводит к виду

,

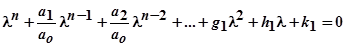после чего делят на множитель первого приближения:

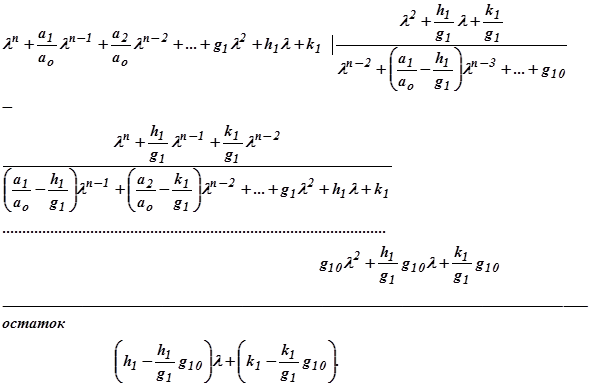
Остаток представляет собой линейный двучлен и характеризует ошибку приближения. Если она недопустимо велика, то исходное уравнение делят на множитель второго приближения 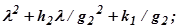снова получают частное 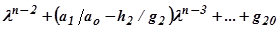и остаток в виде линейного полинома. Если и второе приближение не удовлетворяет, то аналогично выбирают множитель третьего приближения 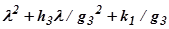и т.д.

Если порядок исходного характеристического уравнения нечётный, то, очевидно, оно имеет по крайне мере один вещественный корень 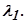При этом делением на множитель 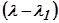понижают на «1» порядок и делают его чётным, после чего, как показано ранее, приближённо определяют множитель второго порядка и т.д.

Если характеристическое уравнение имеет один или несколько вещественных корней, то приближённые их значения легко находятся как точки пересечения кривой Д 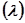с осью абсцисс. Можно подобным путём находить и комплексные корни характеристического уравнения, пользуюсь комплексной плоскостью Д 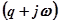и нанося на неё сетку ортогональных кривых: 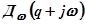при

различных 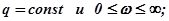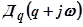при различных .

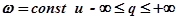Однако этот метод нахождения корней оказывается часто громоздким и длительным.

Обычно удобнее пользоваться для приближённого последовательного определения корней 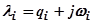характеристического уравнения 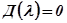годографом Михайлова 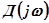. Плоскость 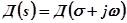и плоскостей корней 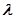взаимосвязаны. Но каждой точке последней соответствует 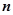точек плоскости корней, где 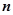- порядок характеристического уравнения. Очевидно, что началу координат плоскости 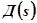отвечает 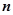корней 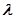. При этом годограф Михайлова 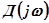отображает на плоскости 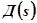мнимую ось плоскости корней, а годограф 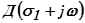отображает вертикаль, сдвинутую вправо на 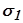относительно мнимой оси на плоскости корней.

Рис.5.89.Схема определения корней характеристического уравнения: а – плоскость 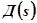; б – плоскость корней

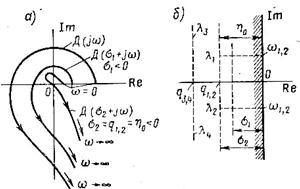Отсюда следует порядок определения корней, произвольно расположенных в левой полуплоскости (рис.5.89). Строим сначала годограф Михайлова 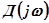(т.е. 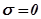). Он, естественно, протекает правильно, так как рассматриваемая САР устойчива. Далее строим 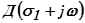, где 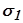выбираем по приближённой оценке степени устойчивости системы. Если этот годограф ещё не пройдёт через начало координат либо начнёт протекать неправильно, то продолжаем дальнейшее построение годографов 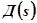методом последовательного приближения до момента 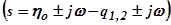, когда 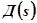пройдёт через начало координат. При этом получим первую пару комплексных корней, зная которые можно понизить на «2» порядок характеристического уравнения, повторить описанное построение и т.д.

Построение переходного процесса по вещественной частотной характеристике. Интегрирование уравнения связывающего переходный процесс системы с её вещественной приведённой частотной характеристикой обычно затруднительно и гораздо удобнее пользоваться приближённым методом В.В. Солодовникова, предложившего аппроксимировать кривую 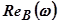кусочно – линейной функцией в виде сторон трапеции или треугольников (рис.5.90, 5.91). При подобной аппроксимации необходимо соблюдать три основные правила:

· все трапеции и треугольники должны иметь одну сторону, расположенную на оси ординат, вторую – расположенную на оси абсцисс;

· алгебраическая сумма площадей трапеций и треугольников должна приблизительно равняться площади, ограниченной кривой 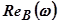и осями координат;

· прямолинейные участки должны по возможности ближе к аппроксимируемым участкам кривой и иметь вид секущих.

В типовой трапеции 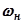- частота равномерного пропускания; 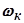- частота пропускания; их отношение 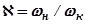меняется от нуля (при 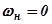трапеция превращается в треугольник) и до единицы (при 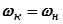трапеция превращается в прямоугольник). В общем случае получим

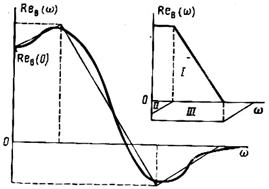
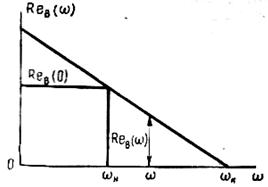Рис.5.90.Аппроксимация вещественной Рис.5.91.Типовая трапеция аппроксимации

частотной характеристики (разбивка на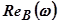

трапеции I, III и треугольник II)

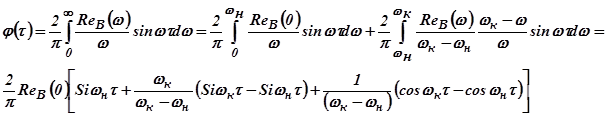
или

.

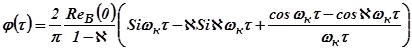Введём безразмерное время 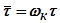. При этом

,

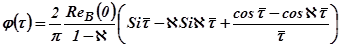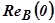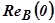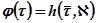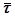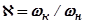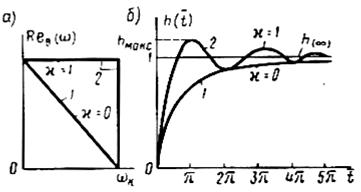
т.е переходный процесс линейно зависит от . Для единичной трапеции [=1] значение определяется двумя аргументами: безразмерным временем и отношением частот , равным коэффициенту наклона верхней стороны. Для так называемой 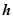- функции имеются специальные таблицы:

.

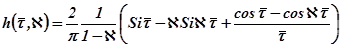Рис.5.92.Предельные случаи для трапеции: а – вещественные частотные характеристики; 1 – превращение трапеции в треугольник; 2 – превращение трапеции в прямоугольник

Рассмотрим предельные случаи. При 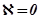, т.е. для треугольника (рис.5.92),

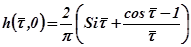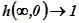; , так как .

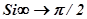При 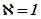, т.е. для прямоугольника (рис.3.54), 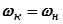и после раскрытия неопределённости 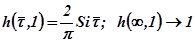, поскольку .

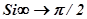Вообще безразмерное время регулирования 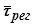, соответствующее трапецеидальной характеристике, изменяется немонотонно, но с общей тенденцией к возрастанию при увеличении .

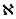При условии подхода на 95% к конечному значению 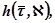т.е к единице (ошибка + 5% конечного значения), 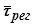находится в пределах от π до 4π, т.е физическое время регулирования находится в интервале от 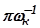до 4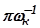(рис.3.55). При этом перерегулирование возрастает с увеличением 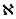от 0 до 1 также от 0 до ~ 18% (рис.5.94 и рис.5.92).

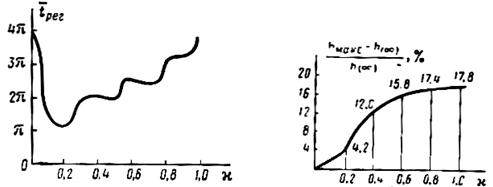
Рис.5.93.Кривая 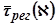для трапецеи- Рис.5.94.Перерегулирование для трапецеи-

дальной характеристики 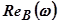дальной характеристики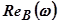

Вместо разбиения вещественной обобщённой частотной характеристики на трапеции можно аппроксимировать её только треугольниками (когда 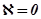) и сделать графо – аналитический расчёт, как и при разбиении на трапеции.

Рассмотрим некоторые характерные свойства вещественных приведённых частотных характеристик систем.

1.При исследовании переходных процессов по формуле 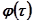и постоянном знаке 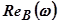можно ограничиться полосой пропускания частот 0<ω<ω_к. Если при ω>ω_к. значение 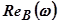<γ (при постоянном знаке), то погрешность определения переходного процесса меньше 0,32γ.

2.Конечное значение φ(τ) после окончания переходного процесса в системе) равно начальному значению : ;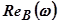

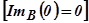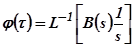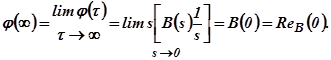
3.Конечное значение переходной функции системы равно начальному значению 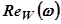, т.е. вещественной собственной частотной функции системы: 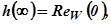поскольку при единичном скачке приведения и собственная передаточные функции совпадают.

Если 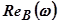- положительная невозрастающая величина, то перерегулирование не превышает 18%. Действительно

.

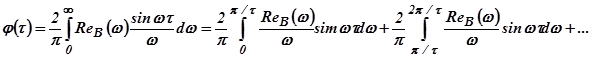4.При положительной линейной убывающей функции 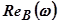переходный процесс, описываемый выражением 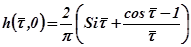, - монотонный, перерегулирования нет.

5.При сходных функциях 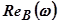, отличающихся лишь масштабом частот, переходные процессы различаются лишь масштабом времени в обратном соотношении: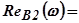 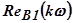величина .

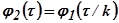6.Острые экстремумы вещественно приведённой характеристики системы при частотах 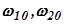предопределяют колебательные процессом приблизительно при тех же частотах.

Построение переходного процесса методом секущих для систем первого порядка.

Рассмотрим дифференциальное уравнение и его решение для подобной статической системы при действии скачкообразного возмущения :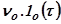

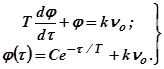
При любом начальном условии ; ; .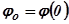

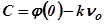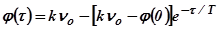Следовательно, .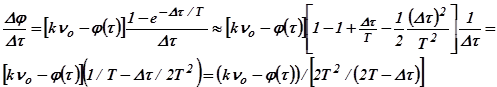

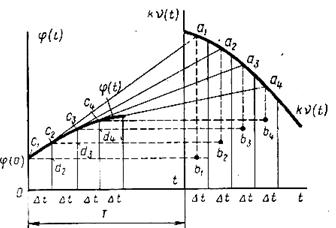
При условии, что слагаемыми с множителями 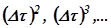и т.д. пренебрегаем, получим

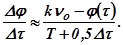
На основании этого выражения строим зависимость 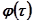- рис.5.95. Для каждого небольшого интервала времени 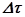возмущение 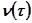считаем постоянным и равным мгновенному значению 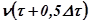на середине этого интервала. В правом поле строим функцию 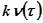с точками 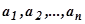, по середине каждого интервала 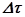, После для 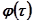сдвигом влево на значение Т. Соединим точку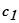 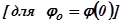с точкой 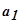. При этом 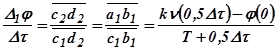, т.е. отрезок 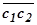изображает приближённо изменение 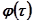на протяжении первого интервала 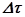. Соединим затем точки 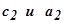. Очевидно, что отрезок 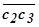характеризует приближённо изменение 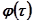на втором интервале 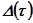[здесь начальное значение 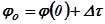и т.д.]. Следовательно, ломанная 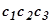… аппроксимирует зависимость 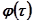для статической системы первого порядка при произвольном возмущении .

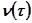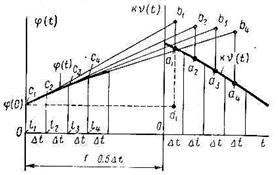
Для астатической (интегрирующей) системы первого порядка

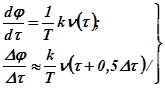
Так же как и в предыдущем случае, делим ось абсцисс на небольшие интервалы времени 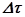и считаем переменное возмущение 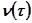, действующее на каждом интервале, постоянным, равным мгновенному значению посередине интервала (рис.5.96). К точкам 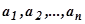добавляем вверх начальные для каждого интервала :

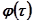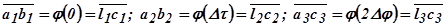и т.д.

Ось 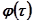смещаем влево от оси 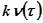на величину 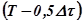. Из треугольника 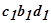видно, что 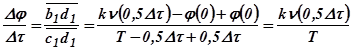. Аналогично получаем и следующие точки ломанной 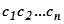аппроксимирующей кривую .

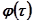Амплитудно-частотная характеристика замкнутой системы. Обычно эта характеристика имеет максимум в области 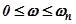. Максимальная ордината этой характеристики, или показатель колебательности М, позволяет судить о колебательности процесса по величине перерегулирования 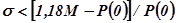, где ; .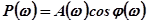

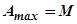С увеличением М колебательность процесса возрастает. Опыт эксплуатации показывает, что при М < 1,3 качество процесса будет удовлетворительным не только при гармоническом, но и при других типовых воздействиях.

АЧХ может быть построена по круговой номограмме типа изображённого на рис.3.47,которая предназначена для определения АФХ замкнутой системы по АФХ разомкнутой системы, выполняемой в координатах номограммы.

Показатель колебательности можно найти не только с помощью АЧХ. В этом случае на сетку окружностей номограммы, построенных для постоянных значений амплитуды А или показателя колебательности М, наносится АФХ разомкнутой системы (рис.5.97, кривая 1). Так как АЧХ определяется по точкам пересечения с окружностями номограммы, то для установления максимального значения ординаты 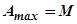следует отыскать окружность с наименьшим радиусом, которая будет касаться АФХ. Индекс этой окружности даёт значение показателя колебательности.

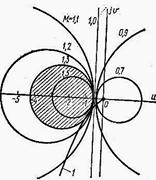Если показатель колебательности М не должен превышать заданную системы не заходила в запретную область, ограниченную окружностью с заданным значением показателя колебательности. На рис.5.97 запретная область заштрихована и определяется окружностью с индексом М=1,3.

Оценка быстродействия системы по АЧХ. Эта оценка может быть осуществлена по резонансной частоте 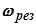, соответствующей максимальной ординате характеристики; частоте среза 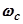,определяемой из условия 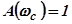, и частоте 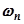,определяющей полосу пропускания замкнутой системы (рис.5.98, а) в соответствии с условием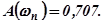

Пусть частотные характеристики замкнутой системы определяются характеристиками идеального фильтра низких частот (рис.5.98, б). В полосе пропускания фильтра, которая примерно совпадает с частотой среза 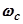, усиления постоянно, а фаза изменяется пропорционально частоте 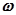. Математическое описание рассматриваемых характеристик имеет вид

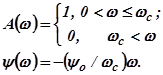
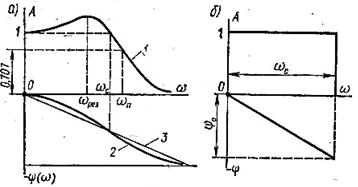Рис.5.98.Частотные характеристики замкнутой системы

Подставляя эти формулы в выражение

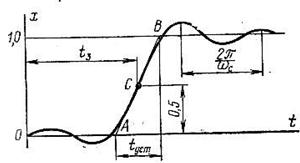
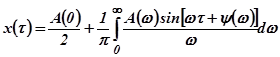(связь между переходной функцией, АЧХ и ФЧХ замкнутой системы), получим после упрощений уравнение для переходной функции 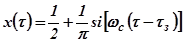, где 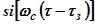- интегральный синус;

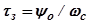- время запаздывания.

График последней функции показана на рис.5.99. Следует иметь в виду, что реакция системы 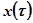для отрицательных моментов времени не равна нулю. Физически это невозможно, так как система до момента приложения воздействия находились в покое. График на рис.5.99 и предыдущая функция широко применяются и являются весьма полезными при установлении связями между частотными характеристиками и переходными процессами.

Время установления, т.е. промежуток времени в течении которого выходного величина изменяется от 0 до 1 с постоянной максимальной скоростью равно 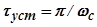, для реальных систем 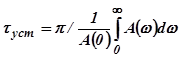. Это уравнение показывает, что с расширением полосы пропускания системы площадь под кривой 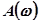возрастает, что приводит к увеличению знаменателя в этом уравнении и уменьшению времени установления, а следовательно, и времени переходного процесса.

Оценка качества по виду логарифмических характеристик. На рис.9.100 для примера показана типовая ЛАЧХ разомкнутой системы с астатических характеристик усиление должно соответствовать неравенству

.

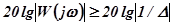Интервал частот 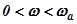, соответствующий последнему выражению, оказывает существенное влияние на статическую точность. Форма ЛАЧХ в этом диапазоне определяет астатизм системы 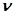.Низкочастотная асимптота АВ (рис.3.60) этой характеристики имеет наклон, равный 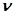20 дБ/дек. Её продолжение до пересечения с осью нулевого усиления определяет коэффициент передачи 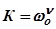. По значению передаточного коэффициента ошибок и, следовательно, ошибки в уставившемся режиме.

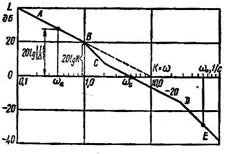
Область средних частот 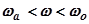, куда входит и частота среза 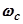, имеет определяющее влияние на форму переходного процесса. Было показано, что по частоте среза можно приближённо судить о времени переходного процесса. В области средних частот к логарифмическим характеристикам предъявляются требования, которые должны обеспечить необходимый запас устойчивости. Логарифмическая АЧХ в интервале средних частот определяется прямой CD (рис.5.100), наклон которой, как правило, берётся равным – 20 дБ/дек.

За пределами граничной частоты 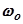, где вещественная частотная характеристика 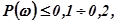логарифмические характеристики оказывают малое влияние на переходный процесс. Область высоких частот 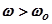(определяется прямой DE) сказывается на начальной части переходного процесса, не имеющей большого практического значения.

Интегральные оценки качества регулирования. Кривая переходного процесса позволяет составить полное суждение о качестве процесса регулирования в данной системе. Косвенную оценку качества регулирования можно получить путём вычисления площади, заключённой между кривой переходного процесса и линией установившегося режима. В этом случае критерием качества будет определённый интеграл по времени от функции, характеризующей разность между действительным и заданным значениями координаты системы. Этот определённый интеграл называется интегральной оценкой, которая в основном используется для монотонных процессов. Для расширения области применения интегрального критерия качества в рассмотрение часто вводят интеграл от квадратичной формы координат системы. Вследствие этого под интегральной оценкой от функции, которая определяет состояние системы и характеризуется в различных комбинациях системными координатами, а также их производными.

Качество системы устанавливается по минимуму интегральной оценки. Различают линейные и квадратичные интегральные оценки.

Линейные интегральные оценки. Определённый интеграл от линейной функции координат системы называется линейной интегральной оценки. Для графика, приведённого на рис.5.101, интегральной оценкой выражение

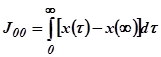, где .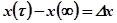

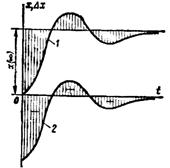
Последний интеграл определяет площадь, ограниченную переходным процессом 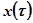(кривая 1) и линией установившегося режима 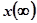, или площадь, заключённая между кривой 2 и осью времени. Он вычисляется по следующей зависимости

.

Это выражение показывает, что величина интегральной оценки зависит от значений параметров системы. Параметры системы следует выбирать по минимуму оценки его, который имеет место при выполнение условия 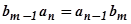(постоянные коэффициенты дифференциального уравнения системы).

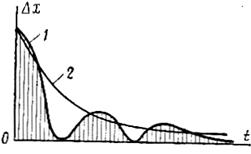
Квадратичные интегральные оценки осуществляются с помощью выражений 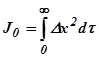. Она может быть использована для любых процессов, так как в рассмотрение принимается только квадратичные значения ординаты переходного процесса и вычисляется площадь под кривой 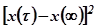(рис.5.102, кривая 1).

Из нескольких процессов наиболее качественным считается тот, который соответствует наименьшей площади или наименьшему значению оценки 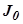. Для устойчивости системы при 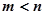квадратичная оценка может быть вычислена по формуле

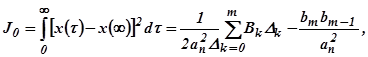
где где ; .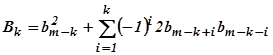

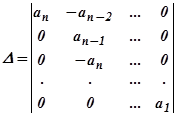Квадратичные интегральные оценки могут быть использованы для выбора параметров системы, обеспечивающих оптимальный переходный процесс, соответствующий минимуму интегральной оценкой.