Для решения линейных дифференциальных уравнений будем использовать преобразование Лапласа.
Преобразованием Лапласа называют соотношение
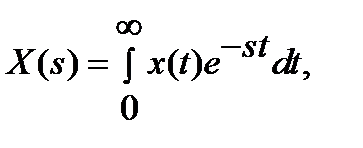 (1)
(1)
ставящее функции x(t) вещественного переменного t в соответствие функцию X(s) комплексного переменного s (s = σ + jω). При этом x(t) называют оригиналом, X(s) — изображением или изображением по Лапласу и s — переменной преобразования Лапласа. Оригинал обозначают строчной, а его изображение — одноименной прописной буквой.
Предполагается, что функция x (t), подвергающаяся преобразованию Лапласа, обладает следующими свойствами:
1) функция x(t) определена и кусочно дифференцируема на интервале [0, ∞);
2) x(t) ≡ 0 при t < 0;
3) существуют такие положительные числа с и М, что │ x(t)│ < Mect при 0 ≤ t < ∞.
Функцию, обладающую указанными свойствами, называют функцией-оригиналом.
Соотношение, определяющее по известному изображению его оригинал, называют обратным преобразованием Лапласа. В нем интеграл берется вдоль любой прямой Re s = σ > с.
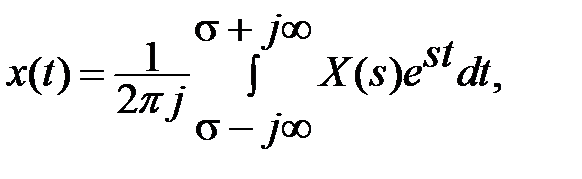 (2)
(2)
Условно прямое и обратное преобразования Лапласа записывают соответственно в виде
X(s) = L{x(t)}, x(t)=L-1{X(s)},
где L — оператор Лапласа, a L -1 — обратный оператор Лапласа. Основные свойства преобразования Лапласа.
1. Свойство линейности. Для любых постоянных α и β
L{αx1(t) +βx2(t)} = aL{x1(t)}+βL{x2(t)},
т. е. преобразование Лапласа от суммы функций равно сумме преобразований слагаемых и постоянные множители можно выносить за знак преобразования.
2. Дифференцирование оригинала. Если 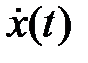 производная является функцией-оригиналом, то
производная является функцией-оригиналом, то
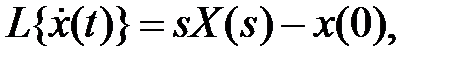
где X(s) = L{x(t)}, 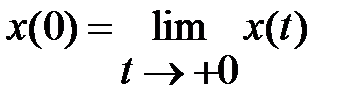 .
.
Здесь запись t → +0 обозначает, что t стремится к нулю, оставаясь положительной (предел справа).
Если п-я производная х (n)(t) является функцией-оригиналом, то
L { х(n) (t)} =snX (s) – s(n -1) x (0) – s(n -2) x (0) - … - x(n -1 ) (0)
Здесь х(k) (0) = lim х(k) (t) k = 0,1,..., n - 1.
t → +0
При x (0) = x (0) =…= x ( n -1)(0) = 0 последняя формула принимает вид
L { х(n) (t)} =snX (s).
Таким образом, при нулевых начальных условиях дифференцированию оригинала соответствует умножение изображения на s.
3. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на s:
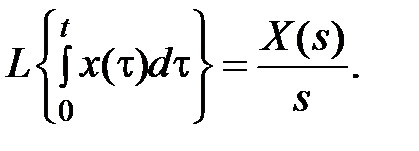
4. Теорема запаздывания. Для любого τ > О
L{x(t - τ)} = e - τSL{x(t)} = e - τSX(s).
5. Теорема дифференцирования изображения. Изображение от произведения t на x(t) равно производной от изображения X(s), взятой с обратным знаком:
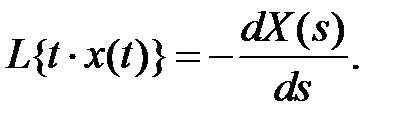
6. Теорема о смещении в комплексной плоскости. Изображение от произведения 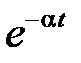 на
на 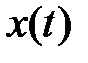 , получаем заменой переменной s на
, получаем заменой переменной s на 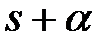 в изображении X(s):
в изображении X(s):
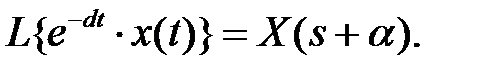
7. Теорема о свертке (умножении изображений). Если x1(t) и x2(t) — оригиналы, a X1(s) и X2(s)— их изображения, то
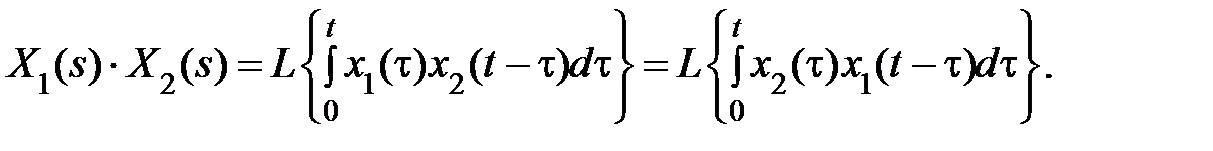
Интеграл в правой части называют сверткой функций x\(t) и x2(i), его обозначают
x1(t) * х2(t):
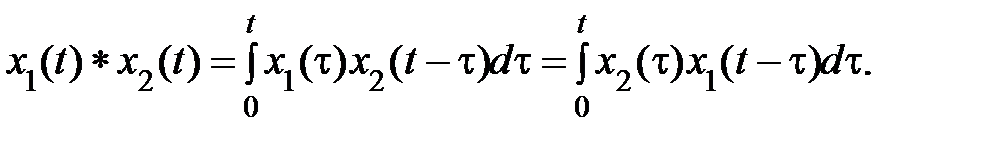
Поэтому
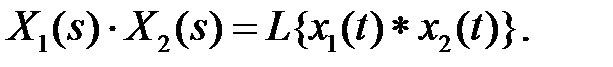
8. Теоремы о предельных значениях. Если х (t) — оригинал, а Х(s) — его изображение, то
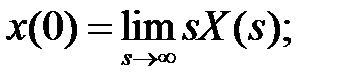
и если существует 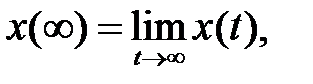 то
то
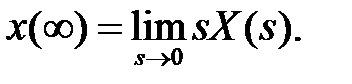
В таблице приведены изображения Лапласа для часто используемых функций
| № | Оригинал x(t) | Изображение X(s) |
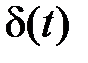 | ||
| 1(t) | 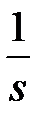 | |
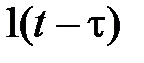 | 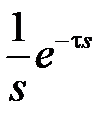 | |
| t | 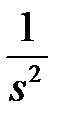 | |
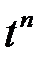 | 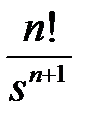 | |
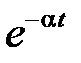 | 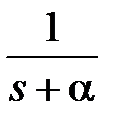 | |
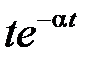 | 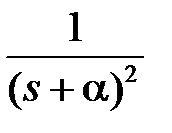 | |
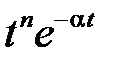 | 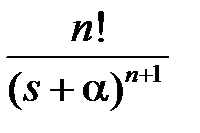 | |
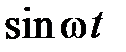 | 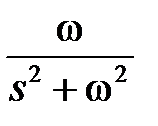 | |
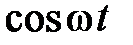 | 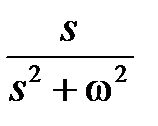 | |
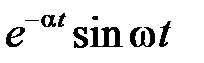 | 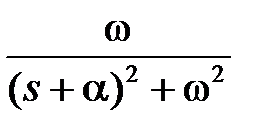 | |
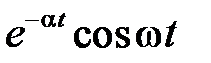 | 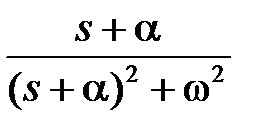 |
Пример 1. Найти изображение для 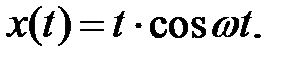
Решение:
Изображение 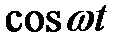 равно
равно 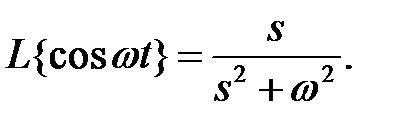
На основании теоремы 5 изображение X(s) будет равно 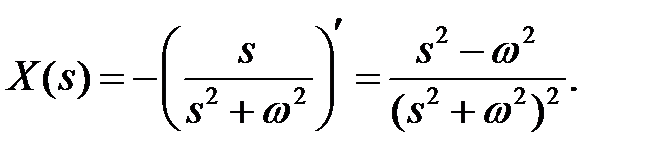
Пример 2. Найти изображение 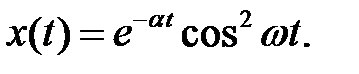
Решение:
Выразим 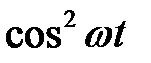 через косинус двойного угла
через косинус двойного угла 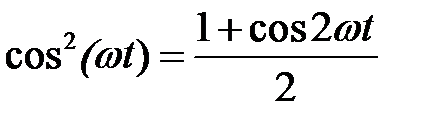
Изображение 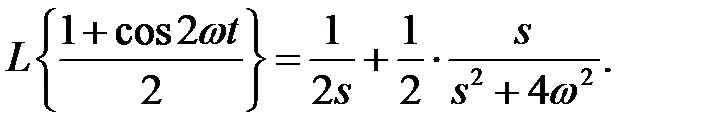
На основании теоремы 6: 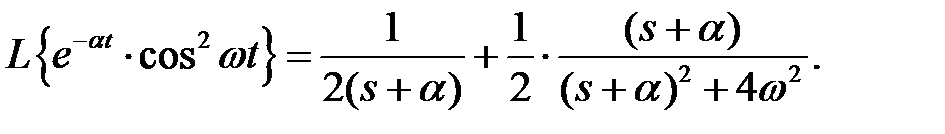
Пример 3. Найти изображение 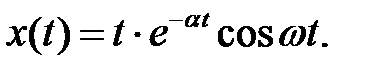
Решение:
Изображение 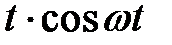 найдено в примере 1.
найдено в примере 1.
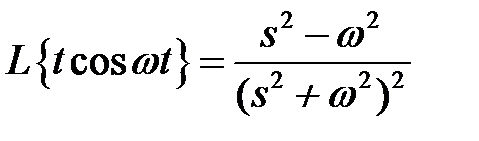
На основании теоремы 6: изображение 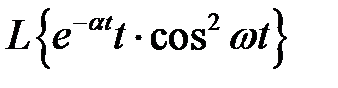 получим, заменив s на
получим, заменив s на 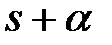 в предыдущем выражении
в предыдущем выражении 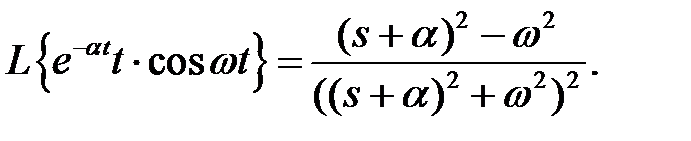
 2015-06-05
2015-06-05 10529
10529
