Свойства дисперсии. В вариационном ряду распределения с равными интервалами дисперсию можно рассчитать, используя «способ моментов»

В вариационном ряду распределения с равными интервалами дисперсию можно рассчитать, используя «способ моментов», который основан на свойствах дисперсии: 1) дисперсия постоянной величины равна нулю; 2) уменьшение всех значений признака на одну и ту же величину А не изменяет дисперсию, следовательно, средний квадрат отклонений можно определить не по заданными значениям признака, а по их отклонениям от какого-либо постоянного числа; 3) уменьшение всех значений признака в k раз уменьшает дисперсию в k² раз, а среднее квадратическое отклонение в k раз, следовательно, все значения признака можно разделить на какое-то постоянное число, определить среднее квадратическое отклонение, а затем умножить его на это постоянное число. 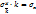. 4) если вычислить 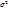от любой величины А, отличающейся от средней (А 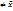), то 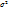будет больше 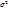, вычисленной от 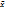(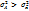), следовательно 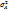= 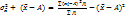, т.е. 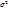имеет свойство минимальности. Если А=0, то 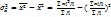. В условиях нормального распределения существует зависимость между величиной 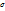и количеством наблюдений: