Газодинамические испытания
Исследование газодинамических процессов обтекания конструкции ЛА позволяет определить силовые нагрузки, связанные с распределением сил аэродинамического давления и трения вдоль внешней поверхности, с возникновением явлений аэроупругости (например, флаттера, бафтинга и т.д.) и акустическим воздействием. С другой стороны, результаты исследований газодинамических характеристик обтекания являются необходимой информацией для оценки тепловых нагрузок, возникающих при аэродинамическом нагреве.
Возможны два метода исследования законов воздействия газа на испытуемый объект:
— сообщение газу некоторой скорости по отношению к неподвижно укрепленному телу;
— сообщение телу некоторой скорости относительно неподвижного газа.
Первый метод реализуется в аэродинамических трубах — установках, в которых создается газовый поток с заданными параметрами для исследования обтекания твердых тел.
Второй метод осуществляется с применением баллистических установок или ракетных трасс.
Так как в обоих случаях испытания главным образом проводятся на моделях, что объясняется ограниченностью энергетических возможностей испытательных центров, рассмотрим основные понятия, связанные с подобием при моделировании в экспериментальной аэродинамике.
Физическое моделирование основывается на физическом подобии явлений.
Геометрическое подобие предполагает пропорциональность сходственных линейных размеров для модели и натуры: IuZln = Ci.
Кинематическое подобие предполагает, что кинематические характеристики сходственных частиц подобных потоков, обтекающих геометрически подобные тела, пропорциональны, т.е. в пропорциональные отрезки времени (tJtH = C2) частицы проходят подобные пути, а скорости и ускорения в сходственных точках пропорциональны и ориентация этих векторов в пространстве одинакова:
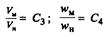
где v — скорость потока; w — ускорение.
Динамическое подобие предполагает, что силы, действующие & сходственных точках, пропорциональны и одинаково ориентированы;
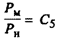
Подобие называется полным, если во всем пространстве, окружающем модель и натуру, соблюдается подобие картин обтекания в целом, т.е. в сходственных пространственно-временных точках выполнены необходимые и достаточные условия подобия.
Если это условие не соблюдается, то подобие называется неполным или частичным. На практике частичное подобие осуществляется довольно часто. При моделировании явления с осуществлением частичного подобия важной задачей является выбор наиболее существенного для данного явления критерия подобия (например, коэффициент сопротивления Cx при определенных значениях практически не зависит от Re и M и достижение высоких значений Re и M при моделировании и определении Cx не нужно).
Важнейшими критериями подобия в гидроаэродинамике являются числа Рейнольдса (Re), Фруда (Fr), Маха (M), Струхаля (Sh).
Если сравниваются потоки, в которых основную роль играют силы вязкости, то числа Рейнольдса для модели и натуры должны быть одинаковы:
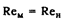
Число Рейнольдса представляет собой отношение инерционных сил к силам вязкости в потоке и характеризует вязкость среды:

где v— скорость потока; i — линейный размер; v — кинематическая вязкость; р. — динамическая вязкость; р — плотность.
Тогда закон подобия с учетом вязкости запишется в виде
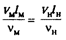
При осуществлении подобия по числу Re можно оперировать тремя параметрами: скоростью V, линейным размером /; кинематической вязкостью V.
Значения параметров и и I ограничены тем, что, во-первых, нельзя увеличивать скорость потока в аэродинамических трубах, поскольку это снижает качество трубы и требует учета сжимаемости воздуха, а ноигорых. нельзя делать очень большие модели.
Чтобы получить большие числа Re, соответствующие натурным условиям, изменяют кинематическую вязкость v, изменяя плотность газа P- Для такого рода экспериментов строят аэродинамические трубы с переменной плотностью сжатого воздуха.
Если в сравниваемых потоках основную роль играют силы тяжести, т.е. предполагается, что среда несжимаемая и невязкая, то основное значение будет иметь число Фруда.
Число Фруда представляет собой отношение инерционных сил к силам тяжести в потоке газа:
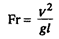
Если числа Фруда для модели и для натурных условий равны (FrM ~ FrH), то говорят, что выполнено частичное подобие по весомости среды, т.е.
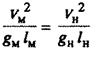
Если gM = gH (ускорение свободного падения для двух потоков), что в подавляющем большинстве опытов выполняется, то линейные размеры модели и натуры пропорциональны квадратам скоростей:
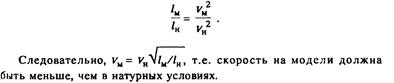
Число Маха представляет собой отношение скорости течения газа к скорости звука в той же точке газообразной среды:
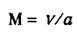
Если два потока, обтекающие модель и натурный объект, являются потоками сжимаемой среды, а сжимаемость зависит от скорости движения потоков и при v> 70 м/с ее надо учитывать, то подобие по сжимаемости будет достигнуто в том случае, когда будет выполняться равенство чисел Маха для модели и натурного изделия, т.е.
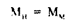
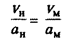
где Vh и Vu — скорости полета натурного изделия и модели соответственно; ан и аи — скорость звука в натурных условиях и в условиях испытаний соответственно.
Число Маха оказывает существенное влияние на характер изменения коэффициентов аэродинамических сил и моментов.
Большой интерес представляет случай, когда надо соблюсти частичное подобие по вязкости и сжимаемости (Re и М), т.е.
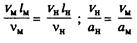
Из второго соотношения следует, что если аи =» аа, то Vv - Vw т.е.
скорости модели и натурного объекта должны быть одинаковы.
Из первого соотношения InZlu- vH/v„, т.е. отношение линейных размеров пропорционально отношению значений кинематической вязкости. Известно, что кинематическая вязкость зависит от давления следующим образом: v = u/p. Если значения динамической вязкости р. у моделируемого и натурного потоков одинаковы (u„~ где ц характеризует силы внутреннего трения и зависит от природы жидкости и его температуры и практически не зависит от давления), то
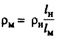
Положив Th ш Tu и используя уравнение состояния (р = pRT), получим
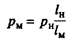
т.е. для обеспечения равенства чисел Re и M модельного и натурного потоков необходимо у модельного потока увеличить статическое давление в рабочей части аэродинамической трубы в — раз. В связи с
этим подобие по критериям Re и M осуществляется при проведении опыта в высокоскоростной трубе переменного давления.
При изучении неустановившихся или периодических движений (колебания крыльев, обтекание вращающегося винта, изменение скорости в следе за телом, образование вихрей и т.д.) подобие осуществляется по числу Струхаля, которое представляет собой отношение
времени протекания процесса T к времени, в течение которого элемент рассматриваемой среды, движущейся со скоростью v, проходит расстояние:
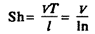
Где v — скорость набегающего потока; T — период протекания нестационарного процесса; l — характерный размер; n — число колебаний в секунду.
При моделировании температурных полей в потоках, обтекающих тело, необходимо осуществить подобие по числу Пекле (Ре):
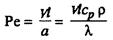
где a = l/(Срр) — коэффициент температуропроводности данного газа; l — коэффициент теплопроводности; р — плотность газа; ср — удельная теплоемкость газа при р = const.
Если числитель и знаменатель до множить на ΔT (разность температур в двух характерных точках), то число Pe можно представить в следующем виде:
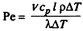
т.е. в виде отношения теплового потока, переносимого жидкостью, движущейся со скоростью v через единицу площади, к тепловому потоку, проходящему через слой толщиной l вследствие его теплопроводности.
В таком виде критерий Pe можно рассматривать как меру относительной роли молярного и молекулярного переноса тепла.
При моделировании температурных и скоростных полей в потоках, обтекающих тело, подобие осуществляется по числу Прандтля, характеризующему отношение интенсивности переноса количества движения вследствие динамической вязкости к интенсивности теплопередачи вследствие теплопроводности:
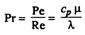
При исследовании гидродинамических сопротивлений в каналах определяющим критерием является число Эйлера, характеризующее соотношение сил давления и сил инерции в потоке:
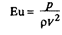
где р — статическое давление; рv2 — скоростной напор.
При изучении течений разреженных газов подобие осуществляется по числу Кнудсена, представляющему собой отношение длины свободного пробега молекулы газа L к характерному линейному размеру l:
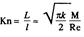
где L — длина свободного пробега молекул; l — характерный линейный размер.
 2014-02-02
2014-02-02 3485
3485
