Способы задания множества
Все элементы некоторого определенного множества обладают некоторым свойством, общим для всех элементов этого множества. Например: множество всех четных чисел; множество всех белых гусей; множество букв русского алфавита.
Тот факт, что х является элементом множества М, записывается так: х Î М. В этом случае говорят, что х входит в М, содержится в М или принадлежит М. Если х не является элементом множества М, то пишут х Ï М.
Определение. Множество считается заданным, если или перечислены все его элементы (только для конечных множеств), или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству.
Первый вариант будем записывать так: М = {m1,m2,..., mk}, например, М= {0, 1}.
Второй вариант задания будем записывать так: М= {b | P(b)}. Такая запись читается как: М состоит из тех (всех) элементов b, которые обладают признаком Р. Например, М = {n | n Î ℕ, n < 5} означает: М составляют только те натуральные числа, что меньше пяти.
Итак, запись М = {х | Р(х)} означает: множество М состоит из всех элементов х, обладающих признаком Р.
Например, запись М = {х | х3 + 3.х2 + 2.х = 0} означает, что множество М содержит только корни данного уравнения, т.е. числа {0; -1; -2}.
Запись А = {х | х ≥ 7, х Î ℕ } читается так: для любых натуральных х, начиная с 7.
Запись B = { b ç b 2 – 1 = 0, b – действительное число} – множество, состоящее из двух элементов, B = {– 1, 1}.
То, что некоторое множество М состоит из элементов x, y, …, t,… записывают так: М ={ x, y,…, t,…}, где многоточием обозначаются не выписанные элементы. Например: A ={ a, b, c }, M ={2,4,6,8,10,…}.
То, что множество состоит из элементов, обладающих некоторым свойством, записывают так: М ={ x: ………}, где на месте многоточия перечисляют свойства элементов. Читается это так: «множество М состоит из элементов х, таких, что…». Например: M ={ x: x = a /2, где а и x Îℤ}.
Для некоторых числовых множеств имеются свои способы записи:
Отрезок числовой оси: [ a, b ]={ x: a ≤ x ≤ b, где a, b, x Îℝ и a ≤ b }.
Интервал: (a, b)={ x: a < x < b, где a, b, x Îℝ и a < b }.
Полуинтервал: (a, b ]={ x: a < x ≤ b, где a, b, x Îℝ и a < b },
или [ a, b)={ x: a ≤ x < b, где a, b, x Îℝ и a < b },
или (-∞, b ]={ x: x ≤ b и b, x Îℝ },
или [ a, +∞)={ x: x ≥ a и a, x Îℝ }.
Определение. Два множества называются равными, если они состоят из одних и тех же элементов, т.е. A = B тогда и только тогда, когда для любого элемента a Î A следует: a Î B, и для любого элемента b Î B следует: b Î A.
Таким образом, множество однозначно определяется своими элементами и не зависит от порядка их записи. Например, множество из трех элементов a, b и c допускает 6 видов записи: { a, b, c }= { a, c, b }= { b, a, c }= { b, c, a }= { c, a, b }= { c, b, a }.
Определение. Если все элементы множества A являются одновременно элементами множества B, то A называется подмножеством или частью множества B.
Пишут A Í B или В Ê А, читается: А входит в В, или А содержится в В, или В содержит А, или В покрывает А. Множество В называется в этом случае надмножеством А. Таким образом, A Í B тогда и только тогда, когда для любого элемента a Î A следует: a Î B.
Очевидно, если A Í B и В Í А, то А = В.
Свойства подмножеств:
a) Пустое множество является подмножеством любого множества: 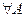 Æ
Æ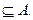
b) Всякое множество является своим собственным подмножеством: 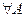
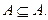
Определение. Если A Í B и А ¹ В, то А называется собственным подмножеством множества В, а В – собственным надмножеством множества А.
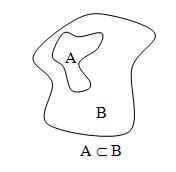
Пишут A Ì B или В É А. Таким образом, A Ì B тогда и только тогда, когда для любого элемента a Î A следует: a Î B, и существует элемент b Î B такой, что b Ï A.
Замечание. Не следует считать равносильными отношения принадлежности 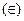 и вхождения одного множества в другое
и вхождения одного множества в другое 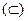 . Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь
. Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь 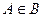 , но
, но 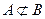 , поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.
, поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.
Определение. Множество всех подмножеств данного множества А называется булеаном А (также степенью множества) и обозначается P (A) или 2 А. Число элементов в булеане конечного множества из n элементов равно 2 n.
Пусть множество А = {1, 2} состоит из двух элементов 1, 2. Тогда множество P (A) включает в себя пустое множество Æ, два одноэлементных множества {1} и {2} и само множество А = {1, 2}, т. е.
P (A) = {Æ, {1}, {2}, {1, 2}}.
Мы видим, что множество P (A) состоит из четырех элементов (4 = 22).
Определение. Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком. Например, множество планет Солнечной системы U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун}.
Заметим, что понятие универсального множества четко не определено, т.е. некорректно. U можно включить в другое множество W, и оно тоже будет универсальным. Например, долго считалось, что множество действительных чисел ℝ универсально (т. е. описывает всю математику), пока не открыли поле комплексных чисел ℂ.
Рассмотрим операции над множествами:
1) Операция включения (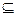 ):
):
Определение. Множество А включается в множество В или множество А является подмножеством множества В (А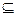 В), если любой элемент множества А содержится в множестве В.
В), если любой элемент множества А содержится в множестве В.
Для графического изображения операции включения множеств используются диаграммы Эйлера-Венна:
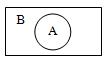
Определение. Множество А строго включается в множество В, если во-первых А является подмножеством В и существует элемент bÎВ, такой что b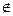 А.
А.
2) Операция объединения ( È ):
Определение. Объединением двухмножеств А и В называется множество С, элементы которого принадлежат хотя бы одному из множеств А и В.
Обозначается С = А È В.
Для графического изображения операции объединения множеств используются диаграммы Эйлера-Венна, где множества представлены как замкнутые области, а результат операции показан заштрихованной частью (см. рис.1).

3) Операция пересечения ( Ç ):
Определение. Пересечением двухмножеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.
Обозначение С = А Ç В.
Диаграмма Эйлера-Венна для пересечения двух множеств показана на рис.2.
Определение Множества называются дизъюнктными (или непересекающимися), если  .
.
4) Операция разности множеств (\):
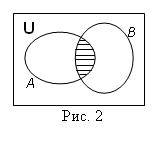
Определение. Разностью двухмножеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.
Обозначается: С = А \ В.
Диаграмма на рис.3.
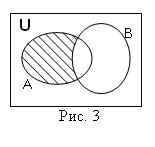
Очевидно, что если 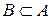 , то
, то 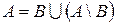 .
.
5) Операция абсолютного дополнения ( 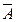 ):
):
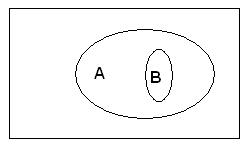
Определение. Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, таким образом, 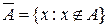 или
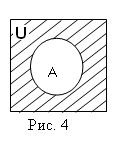
или  U \ A, где U – универсальное множество. Диаграмма Эйлера-Венна на рис.4.
U \ A, где U – универсальное множество. Диаграмма Эйлера-Венна на рис.4.
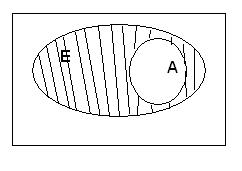
Определение. СЕ называется дополнением множества А относительно множества Е, если А Í Е и CЕ = Е \ A.
6) Операция симметрическая разность( Å ):
Определение. Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, т.е. A Å B = (A \ B)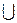 (B \ A). Диаграмма на рис.5.
(B \ A). Диаграмма на рис.5.

Примеры:
1) Пусть 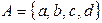 ,
, 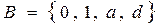 . Тогда
. Тогда 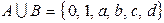 ;
; 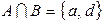 ;
; 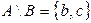 ;
; 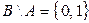 ;
; 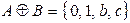 .
.
2) Пусть 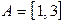 - отрезок,
- отрезок, 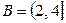 - полуинтервал. Тогда
- полуинтервал. Тогда 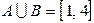 ;
; 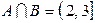 ;
; 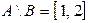 ;
; 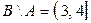 ;
; 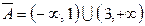 ;
; 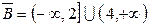 ;
; 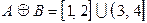 .
.
3) Пусть А – множество прямоугольников, В – множество всех ромбов на плоскости. Тогда 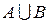 ={все прямоугольники и ромбы};
={все прямоугольники и ромбы}; 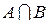 ={все квадраты}; А \ В ={прямоугольники, за исключением квадратов}; В \ А ={ромбы без квадратов}.
={все квадраты}; А \ В ={прямоугольники, за исключением квадратов}; В \ А ={ромбы без квадратов}.
 2014-02-02
2014-02-02 4831
4831
