Понятие множества. Основы теории множеств. Введение

Дискретная математика – часть математики, которая зародилась в глубокой древности. В широком смысле этого слова к дискретной математике относятся как классические разделы математики: алгебра, теория чисел, теория множеств, математическая логика и т.д., так и новые разделы, которые возникли в середине прошлого столетия в связи с появлением ЭВМ. К ним относятся теория графов, теория кодирования и криптография, теория автоматов, теория информации и т.д.

Дискретной математикой называют совокупность математических дисциплин, изучающих свойства абстрактных дискретных объектов. Объектом исследования дискретной математики являются дискретные множества – совокупность, набор некоторых элементов. Поэтому начнем с самого общего глубоко абстрактного раздела этой науки – теории множеств.

Начало созданию теории множеств дал немецкий математик Георг Кантор (1845 – 1918). Понятие «множества» он формулировал следующими словами: «Под множеством понимают объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью» или «множество – это многое, мыслимое в качестве единого».

Определение. Множеством называется объединение в единое целое определенных различимых однотипных объектов, которые называются элементами множества.

Это определение нельзя считать строгим, так как понятие множества является исходным понятием дискретной математики и не может быть определено через другие математические объекты. Понятие «множества» принимается как основное, первоначальное или исходное, не сводимое к другим, более ранним понятиям.

Таким образом, всякое множество состоит из элементов. Множества обозначают большими буквами, например А, В, С, а элементы – маленькими буквами, например, а, b, c.

Определение. Множество, элементами которого являются другие множества, называется классом или семейством.

Примеры множеств:

1) множество гласных букв в русском алфавите;

2) множество людей, присутствующих в данный момент в данной комнате;

3) множество молекул воды в данном конкретном стакане;

4) множество точек, являющихся вершинами некоторого многоугольника и т.д..

Все приведенные примеры множеств обладают одним существенным свойством – эти множества состоят из конечного числа элементов. Конечного в том смысле, что на вопрос «сколько?» всегда можно дать определенный ответ в виде известного (или в данный момент не известного, но, тем не менее, определенного) целого числа.

Определение. Множества, состоящие лишь из конечного числа элементов, называются конечными множествами.

В математике часто приходится сталкиваться с другими – не конечными, или, как принято говорить, бесконечными множествами. Примерами бесконечных множеств могут послужить числовые множества.

Определение. Множество, все элементы которого являются числами, называется числовым множеством.

В дальнейшем мы будем, прежде всего, рассматривать именно такие множества.

Примеры числовых множеств:

1) N– множество всех натуральных чисел – {1,2,3, …};

2) Z – множество всех целых чисел – {…,-2,-1,0,1,2,…};

3) Q – множество рациональных чисел (это числа, которые могут быть представлены в виде дроби, числитель которой – целое число, а знаменатель – натуральное, т.е. x = a / b, где a – целое, b – натуральное);

4) R – множество вещественных (действительных) чисел (это все рациональные и иррациональные числа);

5) C – множество комплексных чисел (это числа, вида х = a +i b, где a и b – вещественные, i–мнимая единица: i²= -1);

6) R² – множество всех упорядоченных пар вещественных чисел (x, y), – вся вещественная плоскость;

7) R ⁿ – n -мерное вещественное пространство, где n – натуральное число, – множество всех упорядоченных последовательностей из n вещественных чисел («энок») или n -мерное вещественное пространство.

Определение. Множество, не содержащее ни одного элемента, называется пустым и обозначается Æ. Пустое множество конечно. Число элементов в пустом множестве равно нулю.

Например, множество целых решений неравенства 5 < х < 6 является пустым.

Пустым будет множество действительных решений уравнений:

х² + 25 = 0 и 5^{2х - 3} = -1.

Определение. Мощностью множества М называется число элементов в него входящих и обозначается |M|.

Например, 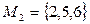, , 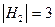где М₂ – множество, Н₂ – мощность множества. Мощность пустого множества равна 0: |Æ| = 0, а мощность множества планет Солнечной системы |U| = 9.